Umgekehrt proportionale Zuordnung 
| Umgekehrt proportional |
a) | Je mehr, desto weniger. |
b) | Je weniger, desto mehr. |
Aufgabe 1: Klick die richtigen Begriffe an.
Umgekehrt proportionale Zuordnungen geben gegenläufiges Wachstum an. Während eine Zahl größer wird, wird die andere . Zum Doppelten einer Größe gehört die der anderen Größe (zum Dreifachen ein ; zur Hälfte das ). In einem Schaubild liegen diese Größen auf einer (siehe unten).Versuche: 0
Aufgabe 2: Klick die richtigen Werte an, damit eine umgekehrt proportionale Zuordnungen entstehen.
| doppelte Anzahl der Maschinen | ↔ | Zeit zur Produktherstellung |
| ein Drittel der Geschwindigkeit | ↔ | Zeit bei gleicher Entfernung |
| halb so viele Mäuse | ↔ | Zeit für den Verbrauch des Futtervorrats |
| dreifache Brettbreite | ↔ | Anzahl an Brettern zur Raumbelegung |
Versuche: 0
Aufgabe 3: Zwei Lastwagen (LKW) benötigen sechs Stunden (h) um einen Schuttberg abzutransportieren. Trage unten den Zeitraum ein, den ein bzw. vier LKWs für die gleiche Menge Abraum brauchen. Nach der richtigen Lösung erscheinen weitere Aufgaben.
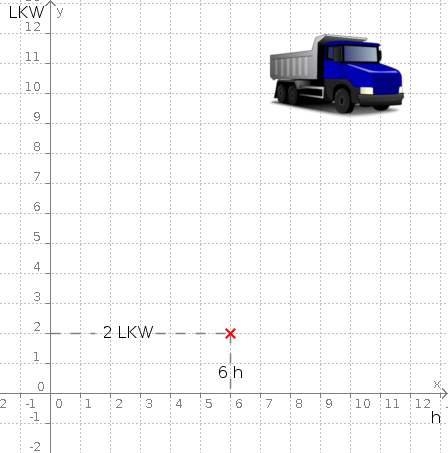
| y (LKW) | 1 | 2 | 4 |
| x (h) | 6 | ||
Info: Wird die Anzahl der LKWs in Aufgabe 3 mit den jeweils benötigten Stunden multipliziert, so erhält man als Ergebnis immer 12. Allgemein formuliert bedeutet das bei umgekehrt proportionalen Zuordnungen: Das Produkt zweier einander zugeordneter Größen bleibt gleich.
Aufgabe 4: Trage den Faktor y ein. Als Ergebnis soll immer die 24 stehen. Bleibt das Produkt von x und y gleich (hier 24), dann stehen beide Größen in einem umgekehrt proportionalen Verhältnis zueinander. Je größer x wird, umso kleiner wird y.
| x | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
| y | ||||||||
| x · y | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
Versuche: 0
Info: Trägt man die Punkte einer umgekehrt proportionalen Zuordnung in ein Koordinatensystem ein, so ergibt sich eine Kurve.
| Aufgabe 5: | a) | Bewege den Punkt C entlang der Kurve. Welche Ähnlichkeiten zur Aufgabe 4 gibt es. Beobachte beim Bewegen die Veränderungen
der grünen Rechenangaben. Dir sollte etwas auffallen. Anschließen kannst du auch den Punkt A bewegen. |
| b) | Schiebe den Punkt A auf die Koordinate (10,6). Bewege Punkt C zu den in der Tabelle aufgeführten x-Koordinaten und übertrage die angegebenen y-Koordinaten in die richtigen Lücken. |
| x | 3 | 4 | 5 | 6 | 10 | 12 | 15 | 20 |
| y | 6 |
Versuche: 0
Aufgabe 6: Ergänze unten die fehlenden Angaben so, dass x mal y als Ergebnis z hat. Das Verhältnis zwischen x und y ist hier umgekehrt proportional. Je größer x wird, desto kleiner wird y. Je kleiner x wird, desto größer wird y.
| a) | |||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
Versuche: 0 | |||||||||||||||||||||||||
| b) | |||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
Versuche: 0 | |||||||||||||||||||||||||
| c) | |||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
Versuche: 0 | |||||||||||||||||||||||||
Aufgabe 7: Trage die fehlenden Werte ein.
| 1. Größe | 1 | 3 | 5 | 7 | 21 | ||||
| 2. Größe | 420 | 105 | 70 | 35 | 14 | ||||
Versuche: 0
Aufgabe 8: Die Werte der ersten und der zweiten Größe stehen in einem umgekehrt proportionalen Verhältnis zueinander. Trage die fehlenden Werte ein.
| · x | · y | ||||||
| a) | 1. Größe | b) | 1. Größe | ||||
| 2. Größe | 2. Größe | ||||||
| : x | : y | ||||||
richtig: 0falsch: 0
Aufgabe 9: Ein Rechteck soll einen Flächeninhalt von 30 cm² haben. Bei welchen Seitenlängen wird diese Fläche erzeugt? Trage unten unterschiedliche Möglichkeiten ein. Achtung: Die Nachkommastellen sind begrenzt! Gerundete Werte zählen nicht.
Info: Die Seitenveränderungen finden in einem umgekehrt proportionalen Verhältnis statt. So viel Mal, wie die Seite a länger (kürzer) wird, muss die Seite b kürzer (länger) werden, um beim gleichen Flächeninhalt zu bleiben.
Angaben in cm
| Rechteck | A | B | C | D | E |
| Seite a | |||||
| Seite b |
richtig: 0 | falsch: 0
Aufgabe 10:
- Trage die richtigen Zahlen unten in die entsprechenden Textfelder ein.
- Wird unten der linke Wert dividiert, dann wird der rechte Wert mit der gleichen Zahl multipliziert.
- Wird unten der linke Wert multipliziert, dann wird rechte Wert mit der gleichen Zahl dividiert.
- Finde die Lösung bei weggeklickter Rechentabelle.
| Aufgabe: | ||||||||||||||||||||||||||||
| Rechnung: |
|
|||||||||||||||||||||||||||
| Antwort: | |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
Aufgabe 11: Frau Behnsen hat eine Schrittlänge von 55 cm. Sie benötigt von ihrem Haus bis zum Bäcker nebenan 72 Schritte. Ihr Mann schafft diese Strecke in 60 Schritten. Welche Schrittlänge hat er?
Der Mann hat eine Schrittlänge von cm.
Versuche: 0
Aufgabe 12: Die Treppe eines Neubaus soll planmäßig aus 16 Stufen von 15 cm Höhe bestehen. Der Bauherr möchte jedoch nur 12 cm hohe Stufen haben. Wie viele Stufen hat die neue Treppe?
Die vom Bauherrn gewünschte Treppe besteht aus Stufen.
Versuche: 0
Aufgabe 13: Jenny kauft 5 m von einem Stoff, dessen Preis 24 €/m beträgt. Wie viel Stoff würde sie für ihr Geld erhalten, wenn der Meter nur 8 € teuer wäre?
Jenny könnte dann m Stoff kaufen.
richtig: 0falsch: 0
Aufgabe 14: Für die Strecke von Talbach nach Bergdorf benötigt ein PKW, der mit durchschnittlich 80 km/h unterwegs ist, 90 min. Wie lange braucht dafür ein LKW, der auf dieser Strecke mit einer Durchschnittsgeschwindigkeit von 60 km/h fährt?
Der LKW benötigt für diese Strecke min.
Versuche: 0
Aufgabe 15: Eine Möbelfirma wird beauftragt, die Büroräume eines Geschäfts einzurichten. Dafür werden 4 Mitarbeiter mit jeweils 18 Arbeitsstunden eingeplant. Nach 6 Stunden verletzt sich einer der Arbeiter so schwer, dass er nicht weiterarbeiten kann. Wie viele Stunden muss jeder seiner Kollegen noch weiterarbeiten?
Jeder der 3 übrigen Mittarbeiter ist nun für weitere Stunden eingeplant, um die Arbeit zu beenden.
Versuche: 0
Aufgabe 16: Eine Fabrik erhält eine dringende Bestellung von elektromechanischen Kunststoffteilen. 16 Maschinen benötigen für den Auftrages 18 Stunden. Nachdem 16 Maschinen 8 Stunden gelaufen sind, helfen 4 zusätzliche Maschinen der gleichen Baureihe, die Fertigungszeit zu verkürzen. Wie viele Stunden Zeitersparnis hat der Betrieb dadurch?
Durch den Einsatz der zusätzlichen Maschinen wird der Auftrag Stunden früher fertiggestellt.
richtig: 0falsch: 0


