Satz des Pythagoras 
 |
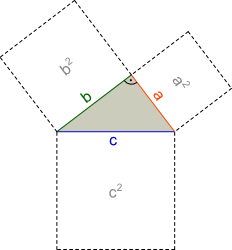
Pythagoras von Samos war ein Philosoph des antiken Griechenlands. Er fand heraus, dass die zwei Quadrate, die an den kurzen Seiten (Katheten) eines rechtwinkligen Dreiecks gebildet werden können, zusammengenommen genau den gleichen Flächeninhalt haben, wie das Quadrat, das an der längsten Seite (Hypotenuse) eines solchen Dreiecks zu bilden ist. Diese Erkenntnis spiegelt sich wider in der Formel: a2 + b2 = c2.
Info: In einem rechtwinkligen Dreieck habe die Seiten bestimmte Bezeichnungen.
|
 |
Aufgabe 1: Klick einen unteren Buttons an und beobachte, was passiert. Klick den nächsten Button, nachdem die grüne Umrandung des vorherigen aufgehoben wurde. Vervollständige danach unten den Satz des Pythagoras.
a² + b² = c²
In einem rechtwinkligen
ist
die
der
-Quadrate
gleich dem Quadrat der
.
Versuche: 0
Aufgabe 2: Bewege die orangen Gleiter der Grafik. Beobachte dabei das Verhältnis der jeweiligen Flächeninhalte zueinander.
Beweise
Aufgabe 3: Du kannst mit den Puzzleteilen der beiden kleinen rechten Quadrate passgenau das große Quadrat unterhalb des rechtwinkligen Dreiecks ausfüllen. Gezogen werden die Teile an den orangen Gleitern.
Aufgabe 4: Mit der unteren Grafik kann die Richtigkeit vom Satz des Pytagoras bewiesen werden. Bewege die orangen Gleiter und versuche diesen Beweis nachzuvollziehen. Klick dann die richtigen Begriffe im unteren Text an.
- Das A und das B haben den gleichen Flächeninhalt.
- Die vier in Quadrat A und Quadrat B haben den gleichen Flächeninhalt.
- Der Flächeninhalt des blauen Quadrats dem Flächeninhalt von Quadrat A dem Flächeninhalt von 4 Dreiecken.
- Der Flächeninhalt der beiden kleinen roten Quadrate dem Flächeninhalt von Quadrat B dem Flächeninhalt von 4 Dreiecken.
- Die Quadrate über den kurzen Dreiecksseiten haben zusammengenommen den Flächeninhalt wie das Quadrat über der langen Dreiecksseite.
- = c2
Versuche: 0
Flächeninhalte berechnen
Aufgabe 5: Notiere den Satz des Pythagoras für Dreiecke mit anderen Seitenbezeichnungen. Achte auf die beiden kurzen und auf die lange Seite.
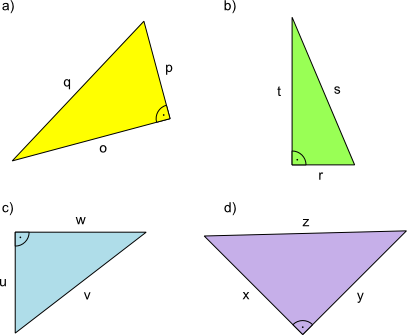
| a) 2 + 2 = 2 | b) 2 + 2 = 2 |
| c) 2 + 2 = 2 | d) 2 + 2 = 2 |
Versuche: 0
Aufgabe 6: Trage die Flächeninhalte der Quadrate A und B ein.
| a) | b) |
| Angaben in cm² | |
| AA = cm2 | AB = cm2 |
richtig: 0falsch: 0
Aufgabe 7: Trage die Flächeninhalte der Quadrate A und B ein.
| a) | b) |
| Angaben in cm² | |
| AA = cm2 | AB = cm2 |
richtig: 0falsch: 0
Aufgabe 8: Trage die Flächeninhalte der Quadrate A, B und C ein.
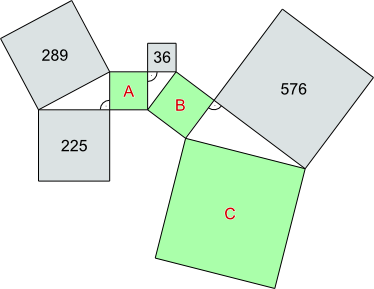
Angaben in cm2
Antwort: AA = cm2; AB = cm2; AC = cm2
Versuche: 0
Aufgabe 9: Die Flächeninhalte von zwei Quadraten über den Seiten eines rechtwinkligen Dreiecks sind vorgegeben. Berechne den Flächeninhalt des Quadrates über der dritten Seite.
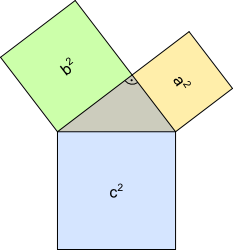
| a) a² = ; | b² = ; | c² = cm² |
| b) c² = ; | a² = ; | b² = cm² |
| c) c² = ; | b² = ; | a² = cm² |
richtig: 0falsch: 0
Aufgabe 10: Trage die Flächeninhalte der Quadrate A und B ein.
| a) | b) |
| AA = cm2 | AB = cm2 |
richtig: 0falsch: 0
Aufgabe 11: Trage die Flächeninhalte der Quadrate A und B ein.
| a) | b) |
| AA = cm2 | AB = cm2 |
richtig: 0falsch: 0
Aufgabe 12: Trage die Flächeninhalte der Quadrate A und B ein.
| a) | b) |
| AA = cm2 | AB = cm2 |
richtig: 0falsch: 0
Aufgabe 13: Zwei Seitenlängen eines rechtwinkligen Dreiecks sind vorgegeben. Berechne den Flächeninhalt des Quadrates über der dritten Seite.
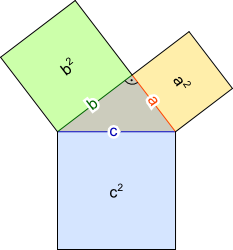
| a) a = ; | b = ; | c² = cm² |
| b) c = ; | a = ; | b² = cm² |
| c) c = ; | b = ; | a² = cm² |
richtig: 0falsch: 0
Aufgabe 14: Quadriere jeweils a, b und c und finde so heraus, ob die Dreiecke mit den folgenden Maßen rechtwinklig sind oder nicht.
Strecken von Flächen berechnen
| Beispiel | |
| • Flächeninhalt(Qu): a² | 16 cm² |
| • Seitenlänge(Qu): √a² = a | √16 cm² = 4 cm |
Aufgabe 15: Klick die richtigen Terme an.
| Formel: a2 + b2 = c2 | |||||
a² = c² - b²; | b² = c² - a²; | c² = a² + b² |
|||
| a = √ | ; | b = √ | ; | c = √ | |
Versuche: 0
Aufgabe 16: Trage die jeweilige Länge der Seite c ein.
| a) | b) |
| Flächenangaben in cm² | |
| x = cm | y = cm |
richtig: 0falsch: 0
Aufgabe 17: Trage die Länge der Seite a und b ein.
| a) | b) |
| Flächenangaben in cm² | |
| a = cm | b = cm |
richtig: 0falsch: 0
Aufgabe 18: Trage die Länge der Seite a und b ein.
| a) | b) |
| a = cm | b = cm |
richtig: 0falsch: 0
Aufgabe 19: Trage die Länge der Seite a und c ein.
| a) | b) |
| c = cm | a = cm |
richtig: 0falsch: 0
Aufgabe 20: Berechne die rote Strecke der jeweiligen Figur auf den mm genau.
gesucht
Antwort: cm
richtig: 0falsch: 0
Aufgabe 21: Trage die fehlenden Seitenlängen der rechtwinkligen Dreiecke ein. Runde die Ergebnisse auf eine Nachkommastelle.
| a) a = cm b = cm c = cm |
b) a = cm b = cm c = cm |
c) a = cm b = cm c = cm |
richtig: 0falsch: 0
Aufgabe 22: Berechne den Umfang des Rechtecks.
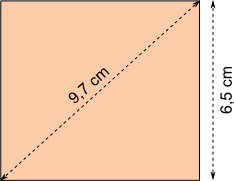
Antwort: Das Rechteck hat einen Umfang von cm
Versuche: 0
Aufgabe 23: Trage für ein Quadrat mit der Seitenlänge a die Länge der Diagonale d ein.
| a) a = cm d = cm Runde auf mm. |
b) a = m d = m Runde auf cm. |
c) a = km d = km Runde auf m. |
richtig: 0falsch: 0
Aufgabe 24: Trage die Länge der Diagonale im Rechteck ein.
| a) a = cm b = cm d = cm Runde auf mm. |
b) a = m b = m d = m Runde auf cm. |
c) a = km b = km d = km Runde auf m. |
richtig: 0falsch: 0
Aufgabe 25: Vom Rechteck ist die Länge der Diagonale d und eine Seitenlänge gegeben. Trage die Länge der zweiten Seite ein.
| a) a = cm b = cm d = cm Runde auf mm. |
b) a = m b = m d = > m Runde auf cm. |
c) a = km b = km d = > km Runde auf m. |
richtig: 0falsch: 0
Aufgabe 26: Berechne den Umfang der Raute.

Antwort: Die Raute hat einen Umfang von cm
Versuche: 0
Aufgabe 27: Ein rechtwinkliges Dreieck ist mit einem gleichseitigen Dreieck zu einer Figur zusammengesetzt. Berechne den Umfang.
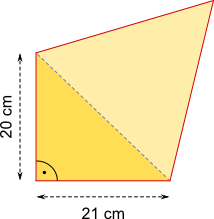
Antwort: Die Figur hat einen Umfang von cm.
Versuche: 0
Aufgabe 28: Gib die Länge der Strecke x an.
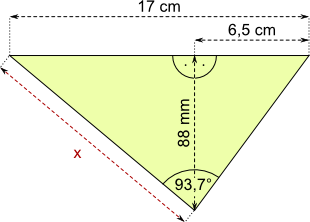
Antwort: Die Strecke x ist cm lang.
Versuche: 0
Aufgabe 29: Trage den Umfang des folgenden Dreiecks ein.
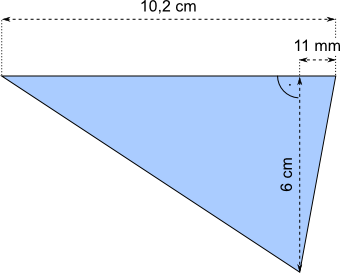
Antwort: Der Umfang beträgt cm.
Versuche: 0
Aufgabe 30: Trage die Länge des Dachsparrens ein, wenn die linke Seite 50 cm übersteht. Berechne auf den cm genau.
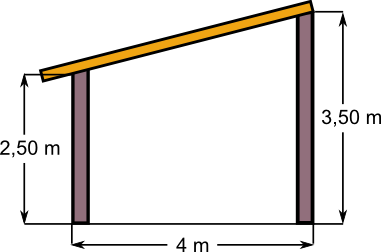
Antwort: Der Sparren hat eine Länge von m.
Versuche: 0
Aufgabe 31: Das Verkehrszeichen "16 % Steigung" bedeutet, dass eine Straße auf 100m Länge um 16 Höhenmeter ansteigt. Wie lang ist eine Straße, die auf 100 m um 16 m ansteigt?
Runde auf zwei Stellen nach dem Komma.

Antwort: Die Straße hat eine Länge von m.
Versuche: 0
Aufgabe 32: Die rot markierten Seile der Brücke müssen ersetzt werden. Wie viel Meter Seil werden dafür benötigt?
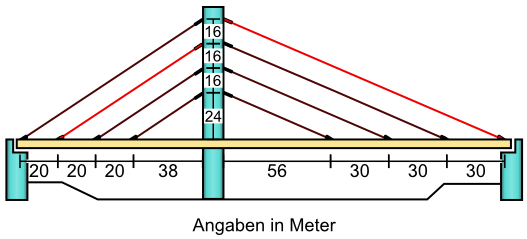
Antwort: Für den Austausch braucht man ,81 m Seil.
Versuche: 0
Aufgabe 33: Eine Leiter ist 5 Meter lang. Bis in welche Höhe reicht sie, wenn aus 1,40 m Entfernung an die Wand gelehnt wird?
Antwort: Die Leiter trifft in m Höhe an die Wand.
Versuche: 0
Aufgabe 34: Ein Schwimmer wird beim Durchqueren eines Flusses von 70 m Breite durch eine starke Strömung 40 m abgetrieben. Trage die geschwommene Strecke ein. Runde auf zwei Nachkommastellen.
Antwort: Der Schwimmer legt eine Strecke von m zurück.
Versuche: 0
Aufgabe 35: An einer Feuerstelle befindet sich eine Astgabel, die sich in 1,05 m Höhe verzweigt. Ein neuer Baumstamm wird darin befestigt, um als Grillgalgen zu dienen. Der Handwerker verankert 34 cm des Stammes in 2,08 m Entfernung zur Astgabel im Boden. Dadurch sind die beiden durch die Gabel getrennten, sichtbaren Baumabschnitte (x) gleich groß. Welche länge hat der Baumstamm?
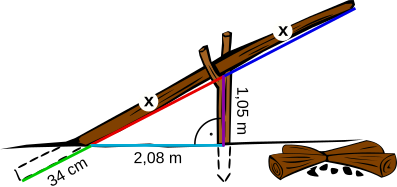
Der neu eingesetzte Baumstamm ist m lang.
Versuche: 0
Aufgabe 36: Ein Baum wurde bei einem Sturm 8 m über dem Boden abgeknickt. Seine Spitze berührt in 15 Metern Entfernung den Boden. Wie hoch war der Baum vor dem Sturm?
Antwort: Der Baum hatte eine Höhe von m.
Versuche: 0
Aufgabe 37: Ein Funkmast ist 102 Meter hoch. In allen 4 Himmelsrichtungen soll 56 Meter vom Fuß des Masten entfernt ein Halteseil 1,5 Meter ins Erdreich hinein betoniert werden. Jedes der 4 Seile wird an einer Manschette befestigt, die sich 12 Meter unter der Funkmastspitze befindet. Wie viel Meter Seil werden insgesamt benötigt?
Antwort: Die 4 Seile haben zusammengenommen eine Länge von m.
Versuche: 0
Aufgabe 38: Um wie viele Kilometer ist der rote Weg länger als der grüne?
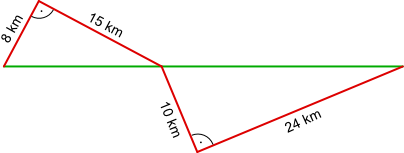
Antwort: Der rote Weg ist km länger als der grüne.
Versuche: 0
Aufgabe 39: Trage den Umfang der roten Figur ein.

Antwort: Der Umfang der Figur beträgt cm.
Versuche: 0
Aufgabe 40: Trage den Umfang der Figur ein.
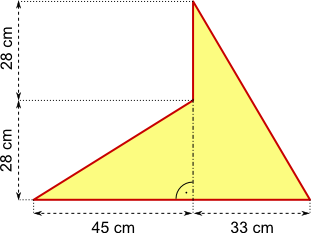
Antwort: Der Umfang der Figur beträgt cm.
Versuche: 0
Aufgabe 41: Wie hoch ist der dargestellte Damm und wie lang ist die Böschung b?
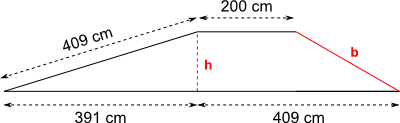
| Antworten: |
| a) Der Damm hat eine Höhe von cm. b) Die Böschung b ist cm lang. |
Versuche: 0
Aufgabe 42: Trage die Länge der unteren Trapezseite ein.
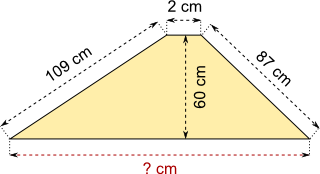
Antwort: Die untere Trapezseite ist cm lang.
Versuche: 0
Aufgabe 43: Trage die Länge der Diagonale des Quadrates ein. Runde auf eine Stelle nach dem Komma.
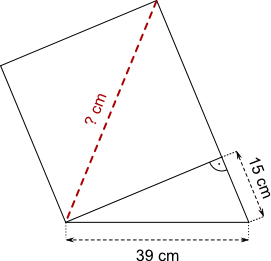
Antwort: Die Diagonale ist cm lang
Versuche: 0
Aufgabe 44: Auf dem Basketballfeld unten sind die Punkte A, B und C markiert. Wie weit sind sie voneinander entfernt? Runde auf Zentimeter.
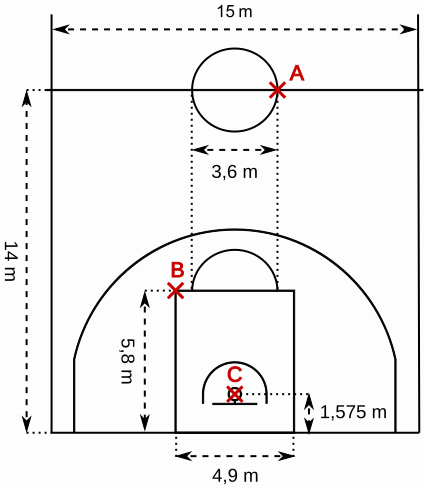
Streckenabstand:
AB = cm, AC = cm, BC = cm
Versuche: 0
Aufgabe 45: Von Punkt P aus werden zwei Tangenten an einen Kreis gelegt. Welche Länge haben die beiden Tangentenabschnitte PQ und PR, wenn der Kreis einen Durchmesser von 48 cm hat und M von P 51 cm entfernt liegt?
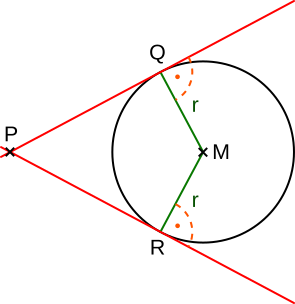
Die zwei Abschnitte haben je eine Länge von cm.
Versuche: 0
Aufgabe 46: Welche Beziehung muss in dem unteren Dreieck zwischen x und s bestehen, damit es a) rechtwinklig, b) stumpfwinklig und c) spitzwinklig ist?
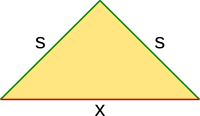
| a) rechtwinklig: √ · |
| b) stumpfwinklig: √ · |
| c) spitzwinklig: √ · |
Versuche: 0
Strecken und Flächeninhalte berechnen
Aufgabe 47: Trage den Flächeninhalt des Dreiecks (a) und des Parallelogramms (b) ein.

| Antworten: |
| a) Das Dreieck hat einen Flächeninhalt von m². b) Das Parallelogramm hat einen Flächeninhalt von m². |
Versuche: 0
Aufgabe 48: Trage den jeweiligen Flächeninhalt der Trapeze ein.

| Antworten: |
|
a) Trapez a hat einen Flächeninhalt von dm². b) Trapez b hat einen Flächeninhalt von dm². |
Versuche: 0
Aufgabe 49: Trage den Flächeninhalt des orangen Dreiecks ein.

Antwort: Der Flächeninhalt des Dreiecks beträgt cm2.
Versuche: 0
Aufgabe 50: Trage den ganzzahligen Wert des Flächeninhalts vom Halbkreis ein.

Antwort: Der Flächeninhalt des Halbkreises beträgt ,8 cm2.
Versuche: 0
Aufgabe 51: Trage den Flächeninhalt der violetten Fläche ein. Runde auf ganze cm2.
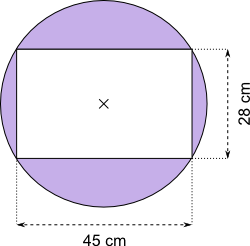
Antwort: Der violette Bereich hat einen Flächeninhalt von cm2
Versuche: 0
Aufgabe 52: Trage die Fläche des Viertelkreises ein. Runde auf eine Stelle nach dem Komma.
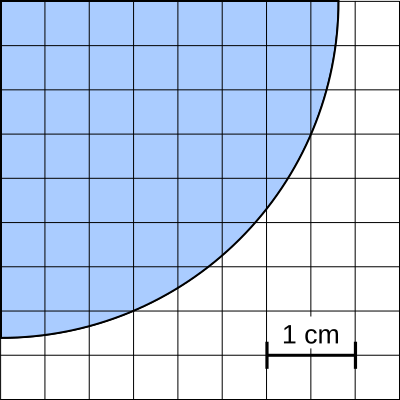
A = cm2
Versuche: 0
Pythagoreisches Fenster
ABCD (1)
Aufgabe 53: Ein rechtwinkliges Dreieck mit den Seitenverhältnissen 3, 4, 5 lässt sich so durch ein quadratisches "Fenster" umschließen, dass die Flächeninhalte der beiden Kathetenquadrate und des Hypothenusenquadrats ganzzahlige Werte ergeben. Ziehe an der orangen Ecke des pythagoräischen Fensters und schätze, wie oft das graue Dreieck in die bunten Flächen hineinpasst.
| In die Fläche mit folgender Farbe | |||||||
| geht das graue Dreieck so oft hinein: |
Versuche: 0
Pythagoreisches Fenster
ABCD (2)
Aufgabe 54: Das "Pythagoräische Fenster" teilt alle neuen Flächeninhalte in ganzzahlige Werte auf. Die roten Zahlen zeigen die Werte der Flächen, die blauen Zahlen die Werte der Strecken an. Kontrolliere die Angaben, indem du hinter die blauen Zahlen die Einheit cm und hinter die roten Zahlen die Einheit cm² setzt. Berechnest du nun mit den blauen Längenangaben eine Fläche, dann ist das Ergebnis die rote Flächenangabe.
Hilfe: Länge und Breite eines Gitterkästchens betragen in diesem Fall ![]() cm.
cm.
von Hartwig Runge alias Ingo Graf
Strecken und Flächen von Räumen berechnen
Aufgabe 55: Berechne die rote Strecke des jeweiligen Körpers auf den mm genau.
|
Pyramide
Angaben in cm
(Dreieckshöhe) Länge = cm |
Quader
Angaben in cm
(Raumdiagonale) Länge = cm |
Kegel
Angaben in cm
(Höhe) Länge = cm |
richtig: 0falsch: 0
Aufgabe 56: Trage die Länge der folgenden Strecken des Quaders ein. Runde auf eine Nachkommastelle.
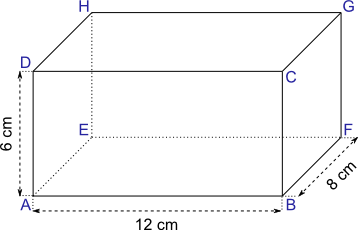
| A F | = cm; | C F | = cm; | A G | = cm; |
Versuche: 0
| Aufgabe 57: Trage die Höhe der Pyramide ein. ( | A C | = 112 cm; | A S | = 106 cm) |
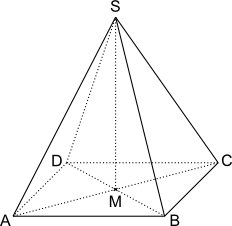
Antwort: Die Pyramide ist cm hoch.
Versuche: 0
Aufgabe 58: Berechne die Oberfläche der folgenden Pyramide. Beachte die Größenangaben. Runde auf ganze dm².
Maße in cm
O = dm²
richtig: 0falsch: 0
Aufgabe 59: Trage den Oberflächeninhalt der Pyramide ein, die unten als Netz dargestellt ist. Runde auf eine Nachkommastelle.
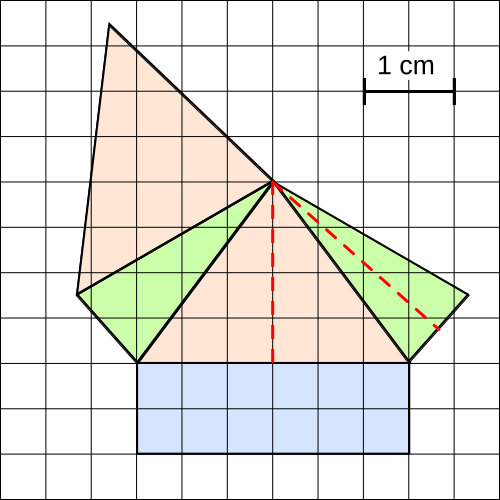
O = cm2
Versuche: 0
Aufgabe 60: Von den Größen eines Walmdaches sind gegeben: a = 12 m; b = 6 m; c = 5 m und d = 9 m. Wie hoch ist das Walmdach (hW)? Runde auf cm.
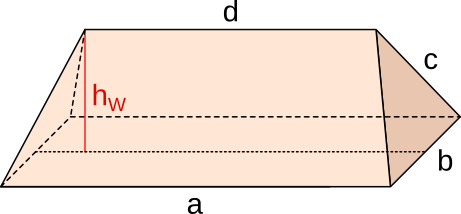
Das Dach hat eine Höhe von m.
Versuche: 0
Aufgabe 61: Trage den Flächeinhalt des orangen Dreiecks unten ein.
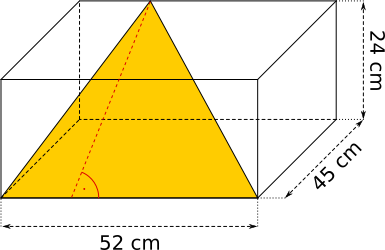
Die Dreiecksfläche beträgt cm2.
Versuche: 0
Aufgabe 62: Bei einem Kegel ist die Seitenlinie (s) und der Umfang (u) lang. Wie groß ist sein Volumen? Trage den ganzzahligen Wert des Ergebnisses ein.
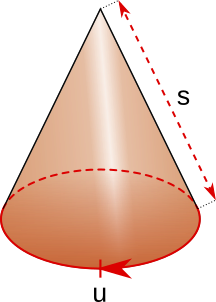
Der Kegel hat eine Volumen von , cm3.
richtig: 0falsch: 0
Aufgabe 63: Ein Würfel mit einer Kantenlänge a von wird so zersägt, dass als neue Fläche ein gleichseitiges Sechseck entsteht. Welchen Flächeninhalt hat dieses Sechseck? Trage den ganzzahligen Teil des Ergebnisses ein.
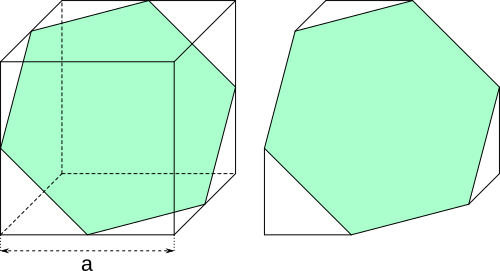
Der Flächeninhalt des Sechsecks beträgt , cm²
richtig: 0falsch: 0
Aufgabe 64: Ein Tetraeder aus vier gleichseitigen Dreiecken hat eine Kantenlänge (a) von . Wie groß ist sein Oberflächeninhalt? Trage den ganzzahligen Wert des Ergebnisses ein.
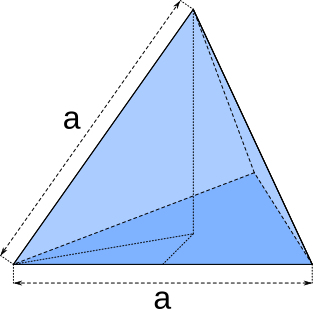
Der Tetraeder hat eine Oberfläche von , dm2.
richtig: 0falsch: 0
Aufgabe 65: Eine Pyramide hat als Grundfläche ein gleichseitiges Sechseck. Eine Sechseckseite (a) ist lang. Die Höhe (h) der Pyramide beträgt . Berechne den Oberflächeninhalt dieser Pyramide. Trage den ganzzahligen Wert des Ergebnisses ein.
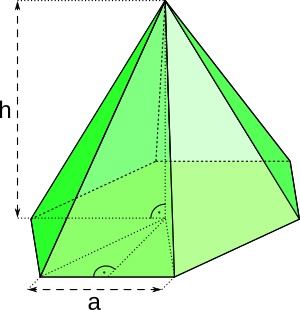
nicht maßstabsgetreu
Die Pyramide hat einen Oberflächeninhalt von , cm2
richtig: 0falsch: 0

