Terme umformen
Hier kannst du ...- Terme vereinfachen (A 1 - A 18),
- Klammern auflösen, ausmultiplizieren und Terme zusammenfassen (A 19 - A 49),
- Summenterme in Produkte umwandeln (Ausklammern) (A 50 - A 52).
Terme vereinfachen
Um Rechnungen übersichtlicher zu machen, werden Terme (Rechenausdrücke) auf unterschiedliche Art und Weise vereinfacht.
- Bei Additionen und Subtraktionen können gleichartige Variablen zusammengefasst werden.
x + x + x + x = 4x
2a + 3a + 4b - b = (a + a) + (a + a + a) + (b + b + b + b) - (b) = 5a + 3b
-
Bei Multiplikationen werden die Zahlen multipliziert. Die Variablen bleiben als Faktoren vorhanden.
3y · 2z = 3 · y · 2 · z = (3 · 2) · y · z = 6yz
-
Bei Divisionen ist es möglich, am Bruchstrich zu kürzen.
6ab : (2b) = 3\6 · a · /b1 = 3 · a = 3a 1\2 · /b1
Beachte beim Vereinfachen die Punkt-vor-Strich-Regel und die Klammern-zuerst-Regel.
Beim Eintrag in die Textfelder niemals ein Malzeichen (2 * y) sondern immer die kurzschreibweise (2y) verwenden!
Aufgabe 1: Ergänze für die Strecke a) AB; b) CD und c) EF die dazugehörigen Terme.
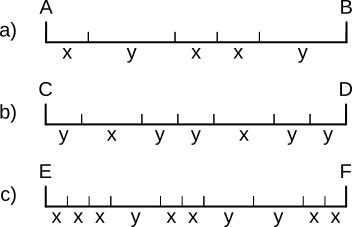
a) x + y
b) x + y
c) x + y
Versuche: 0
Aufgabe 2: Die Strecke AC kann durch den Term 4x + 3y und die Strecke DF durch den Term 2x + 5y bestimmt werden. Ergänze den Term zur Bestimmung der Strecke BC und der Strecke EF.
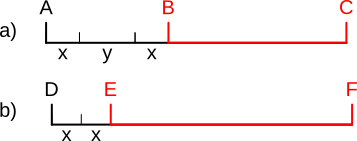
|
BC = x + y EF = y |
Versuche: 0
Aufgabe 3: Fasse gleiche Variable und alleinstehende Zahlen zusammen.
| a) | + + + + = | b) | + + - = |
| c) | + - = | d) | + + - + = + |
| e) | + + = + |
richtig: 0falsch: 0
Aufgabe 4: Addiere die Nachbarsteine.
| 03 | 04 | ||||||
| 00 |
01 |
02 | |||||
richtig: 0falsch: 0
Aufgabe 5: Ergänze den fehlenden Term.
| a) |
| b) |
richtig: 0falsch: 0
Aufgabe 6: Trage die fehlenden Zahlen ein.
| a) |
| b) |
richtig: 0falsch: 0
Aufgabe 7: Klick in den oberen Fenstern der drei mittleren Häuser die zum Zug gehörigen vereinfachten Terme an. Nach drei fehlerhaften Auswertungsversuchen startet die Animation erneut.



|
|
Aufgabe 8: Trage die Produkte der Zahlen in die entsprechenden Textfelder ein und klicke die richtige Buchstabenfolge an.
| a) = | b) = |
| c) = | d) = |
richtig: 0falsch: 0
Aufgabe 9: Multipliziere die Nachbarsteine.
| 13 | |||||||
| 10 | 11 | 12 | |||||
richtig: 0falsch: 0
Aufgabe 10: Vollständige den Term, der den Umfang (u) der folgenden Figur wiedergibt.

u = x
Versuche: 0
Aufgabe 11: Trage die richtigen Werte ein.
| a) 2x · = 2x |
| b) 2x · = 2x |
richtig: 0falsch: 0
Aufgabe 12: Die folgende Box ist mit einem Geschenkband umwickelt. Für die Schleife werden 40 cm zusätzlich veranschlagt. Vervollständige den Term für die Länge des Bandes.

Längenterm: a + b + c +
Versuche: 0
Aufgabe 13: Ergänze den gekürzten Bruch und das Ergebnis.
| (8x) : 4 = | 8x | = | x | = x |
| 4 | 1 |
richtig: 0falsch: 0
Aufgabe 14: Klick so lange auf die grauen Felder, bis die passenden Terme erscheinen.
| a) | = | 6x | = | 2 |
= | ||
| 3x | 1 |
| b) | = | 6x | = | 2 |
= | ||
| 3x | 1 |
| c) | = | 6x | = | 2 |
= | ||
| 3x | 1 |
richtig: 0 | falsch: 0
Aufgabe 15: Ordne die Terme dem entsprechend vereinfachten Term zu.
| a) | b) |
Aufgabe 16: Klick den richtigen vereinfachten Term an.
| 1 |
| 2 |
| 2x | 2 | 1 | |
| x |
richtig: 0 | falsch: 0
Aufgabe 17: Klick die passenden vereinfachten Terme an.
a) Addition
| + | 2x | z | 4 |
3x |
| 5x | ||||
| 4z | ||||
| x + z |
Versuche: 0
b) Subtraktion
| - | x | y | 1 |
3y |
| 3x | ||||
| 4y | ||||
| 5x + 3y |
Versuche: 0
c) Multiplikation
| · | 10 | b | 2d | 0,5 |
| 2a | ||||
| 4 | ||||
| 5c |
Versuche: 0
d) Division
| : | 2 | x | (2x) | 4 |
| 28x | ||||
| x | ||||
| 4x |
Versuche: 0
Aufgabe 18: Trage die richtigen Werte der vereinfachten Terme ein.
|
a) = · · b) = · · |
richtig: 0falsch: 0
Klammern auflösen, ausmultiplizieren und Terme zusammenfassen
| Plusklammer (Klammer einfach weglassen) |
|
| a + (b + c) = a + b + c | a + (b - c) = a + b - c |
| Minusklammer (Vorzeichen in der Klammer umgekehren) |
|
| a - (b + c) = a - b - c | a - (b - c) = a - b + c |
| Multiplikationsklammer (Jeden Klammerwert mit dem Faktor der Klammer multiplizieren) |
|
|
a · (b + c) = ab + ac (a + b) · c = ac + bc |
a · (b - c) = ab - ac (a - b) · c = ac - bc |
| Divisionsklammer (Jeden Klammerwert durch den Divisor teilen) |
|
| (a + b) : c = a : c + b : c | (a - b) : c = a : c - b : c |
| Klammer · Klammer (Jedes Glied der ersten Klammer mit jedem Glied der zweiten Klammer multiplizieren) |
|
| (a + b) · (c + d) = ac + ad + bc + bd | |
| (a + b) · (c - d) = ac - ad + bc - bd | |
| (a - b) · (c + d) = ac + ad - bc - bd | |
| (a - b) · (c - d) = ac - ad - bc + bd |
Aufgabe 19: Trage die fehlenden Daten ein.
|
a) 10 + (3 + 2) = = c) 5a + (b + a) = = a + b e) 10 + (3 - 2) = = g) 5a + (b - a) = = a + b |
b) 10 - (3 + 2) = = d) 5a - (b + a) = = a - b f) 10 - (3 - 2) = = h) 5a - (b - a) = = a - b |
Versuche: 0
ACHTUNG! In den folgenden Aufgaben ist der zusammengefasste Term einzutragen. Die Auflösung der Klammer muss vorher gedanklich oder im Heft durchgeführt werden.
Aufgabe 20: Löse die Klammern schriftlich auf. Trage dann die fehlenden Zahlen und Rechenzeichen ein.
|
a) = b) = a c) = x y d) = x |
richtig: 0 | falsch: 0
Aufgabe 21: Trage das fehlende Pluszeichen(+) oder das Minuszeichen(-) richtig ein.
| a) | |||
| b) | |||
| c) | |||
| d) | |||
richtig: 0falsch: 0
Aufgabe 22: Löse die Klammern schriftlich auf. Trage dann die fehlenden Zahlen und Rechenzeichen ein.
|
a) = p q b) = r s c) = x y |
richtig: 0falsch: 0
Aufgabe 23: Löse die Klammern schriftlich auf. Trage dann die fehlenden Zahlen und Rechenzeichen ein.
|
a) = x y z b) = u v w |
richtig: 0falsch: 0
Aufgabe 24: Löse die Klammern schriftlich auf. Trage dann die fehlenden Zahlen und Rechenzeichen ein.
|
a) = a2 a b b) = a b2 b |
richtig: 0falsch: 0
Aufgabe 25: Der Flächeninhalt des rot umrandeten Rechtecks lässt sich aus den Flächeninhalten des gelben und grünen Rechtecks berechnen. Ergänze den Term zu einer richtigen Gleichung. Du kannst mehrere Beispiele erzeugen und nachrechnen.
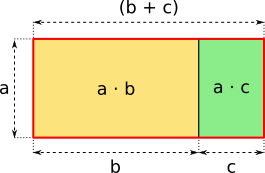
Fläche des Rechtecks:
a · (b + c) = · b + · c
Versuche: 0
Aufgabe: 26 Der Flächeninhalt des rot umrandeten Rechtecks lässt sich aus dem Flächeninhalt eines größeren Rechtecks berechnen. Ergänze den Term zu einer richtigen Gleichung. Du kannst mehrere Beispiele erzeugen und nachrechnen.
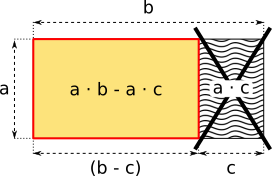
Fläche des Rechtecks:
a · (b - c) = · b - · c
Versuche: 0
Aufgabe 27: Löse die Klammern schriftlich auf. Trage die fehlenden Werte und Rechenzeichen ein. Die jeweiligen Variablen sind bereits vorgegeben.
|
a) = b) = c) = d) = |
richtig: 0falsch: 0
Aufgabe 28: Löse die Klammern schriftlich auf. Trage die fehlenden Werte und Rechenzeichen ein. Die jeweiligen Variablen sind bereits vorgegeben.
|
a) = b) = c) = d) = |
richtig: 0falsch: 0
Aufgabe 29: Löse die Klammern schriftlich auf. Trage die fehlenden Werte und Rechenzeichen ein. Die jeweiligen Variablen sind bereits vorgegeben.
| a) | p |
| b) | q |
| c) | r |
| d) | s |
richtig: 0falsch: 0
Aufgabe 30: Löse die Klammern schriftlich auf. Trage die fehlenden Zahlen und Rechenzeichen ein.
|
a) = a b b) = x y c) = u v w |
richtig: 0falsch: 0
Aufgabe 31: Trage die richtigen Werte in die Lücken.
| a) | |
| b) | |
richtig: 0falsch: 0
Aufgabe 32: Erstelle schriftlich den Term für die Kantenlänge (a) und das Volumen (b) des Quaders. Trage dann unten die fehlenden Werte ein.
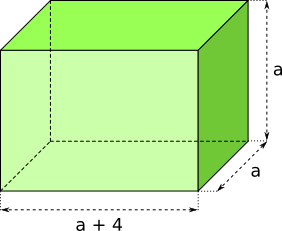
a) Kantenlänge des Quaders:
· a + · (a + 4) = a +
Versuche: 0
b) Volumen des Quaders:
a · a · () = a + a
Versuche: 0
Aufgabe 33: Erstelle schriftlich den Term für den Umfang (a) und den Flächeninhalt (b) des Rechtecks. Trage dann unten die fehlenden Werte ein.

a) Umfang des Rechtecks:
· x + · (3x + 7) = x +
Versuche: 0
b) Flächeninhalt des Rechtecks:
(x + ) · x = x + x
Versuche: 0
Aufgabe 34: Erstelle schriftlich den Term für den Umfang (a) und den Flächeninhalt (b) des Rechtecks. Trage dann unten die fehlenden Werte ein.

a) Umfang des Rechtecks:
· x + · (3 · (x + 7)) = x +
Versuche: 0
b) Flächeninhalt des Rechtecks:
(3 · (x + 7)) · x = (x + ) · x = x + x
Versuche: 0
Aufgabe 35: Erstelle schriftlich den Term für den Umfang der Fläche. Trage dann unten die fehlenden Werte ein.

Flächenumfang:
· x + · (x + 1) + 2 · (x - 1) = x
Versuche: 0
Aufgabe 36: Die fett gedruckten Werte geben den Flächeninhalt an. Trage die richtigen Seitenlängen in die Lücken ein.
| x | ||
| 3x | 3 |
richtig: 0falsch: 0
Aufgabe 37: Fülle die Lücken richtig aus.
| 3x | |
| 15x² | |
| 3xy | |
| 4 |
Versuche: 0
Aufgabe 38: Erstelle schriftlich den Term für die Kantenlänge (a) und das Volumen (b) des Quaders. Trage dann unten die fehlenden Werte ein.
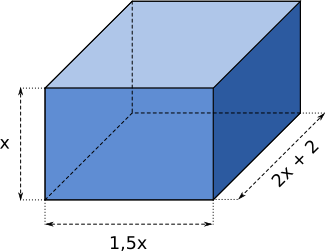
a) Kantenlänge des Quaders:
· x + · 1,5x + · (2x + 2) = x +
Versuche: 0
b) Volumen des Quaders:
x · x · (x + ) = x3 + x
Versuche: 0
Aufgabe 39: Erstelle schriftlich den Term für die Kantenlänge des Körpers. Trage dann unten die fehlenden Werte ein.
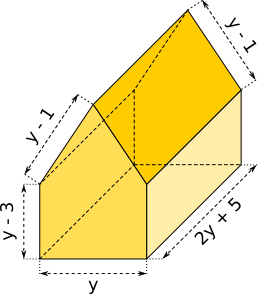
Kantenlänge des Körpers:
· y + · (2y + 5) + · (y - 1) + · (y - 3) = y +
Versuche: 0
Aufgabe 40: Erstelle schriftlich den Term für den Umfang der Fläche. Trage dann unten die fehlenden Werte ein.

Flächenumfang:
x · π + x
Versuche: 0
Aufgabe 41: Trage die fehlenden Daten ein.
|
a) 5a + 5b = (a + b) b) 4x + 8y = (x + 2y) c) 6ax + 6ay = (x + y) d) 2a · (6b + 4c - 12) = 12b + 8c - a |
Versuche: 0
Aufgabe 42: Löse die Klammern schriftlich auf. Trage die fehlenden Zahlen und Rechenzeichen ein.
|
a) = r s t u b) = a b c |
richtig: 0falsch: 0
Aufgabe 43: Multipliziere die Summen. Trage die entsprechenden Produkte in die richtigen Felder ein. Ergänze das ausmultiplizierte Ergebnis mit den richtigen Werten.
| 5 | z | |
| x | ||
| 1 |
Ausmultipliziertes Ergebnis:
xz + x + z +
richtig: 0falsch: 0
Aufgabe 44: Multipliziere die Summen. Klicke die richtigen Produkte in den Felder an. Ergänze das ausmultiplizierte Ergebnis mit den richtigen Werten.
| x | 5 | |
| 2 | ||
| x |
Ausmultipliziertes Ergebnis:
x² + x +
Versuche: 0
Aufgabe 45: Multipliziere die Summen. Klicke die richtigen Produkte in den Felder an. Ergänze das ausmultiplizierte Ergebnis mit den richtigen Werten.
| 2c | d | |
| a | ||
| b |
Ausmultipliziertes Ergebnis:
2a + a + bc +
Versuche: 0
Aufgabe 46: Löse die Klammern schriftlich auf. Trage die fehlenden Daten ein und klick die richtigen Rechenzeichen an.
|
a) (x + 3)(4 + y) = x y 3 b) (x + 3)(4 + y) = x y 3 |
richtig: 0falsch: 0
Aufgabe 47: Löse die Klammern schriftlich auf. Trage die fehlenden Daten ein und klick die richtigen Rechenzeichen an.
|
a) (3a + 2b) · (5c - 2d) = a ad b bd b) (-4a + 2b) · (-3c + 5d) = ac a bc b c) (-5a - 3b) · (-2c + 4d) = a ad b bd |
Versuche: 0
Aufgabe 48: Löse die Klammern schriftlich auf. Trage die fehlenden Daten ein und klick die richtigen Rechenzeichen an.
(3a + 2b) · (5c - 2d) = a ad b bd
richtig: 0falsch: 0
Aufgabe 49: Löse die Klammern schriftlich auf. Trage die fehlenden Daten ein und klick die richtigen Rechenzeichen an.
= x y 3
richtig: 0falsch: 0
Aufgabe 50: Ordne die richtigen Klammerterme zu.
| a) 2x + 18 y = | b) 2x + 18 y = |
| c) 2x + 18 y = | d) 2x + 18 y = |
| e) 2x + 18 y = | f) 2x + 18 y = |
richtig: 0falsch: 0
Aufgabe 51: Trage die richtigen Werte ein.
| a) 7 + 14x = ( + x) | b) 8xy + 32y = (x + ) |
| c) n + 3nm = ( + ) | d) 6a - 84b = ( - ) |
| e) 9xy - 81xz = ( - ) | f) 7ab - 21 = ( - ) |
Versuche: 0
Aufgabe 52: Trage die richtigen Werte ein.
| a) xy - 3,5y² = ( - ) | b) a² + a = ( + ) |
| c) 0,7a² - 0,7ab = ( - ) | d) 5x²y - 2xy² = ( - ) |
| e) 15p² + 25pq = ( + ) | f) 54a²b - 36ab² = ( - ) |
Versuche: 0

