Pyramiden- und Kegelstumpf
|
Quadratischer Pyramidenstumpf
|
Kegel
|
|||||||||
 |
 |
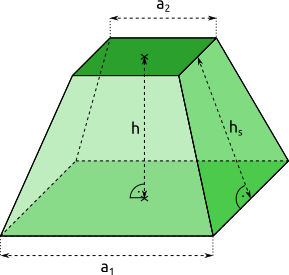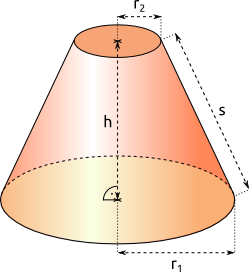Aufgabe 1: Trage das Volumen des quadratischen Pyramidenstumpfes ein. Runde auf eine Nachkommastelle.
Der Pyramidenstumpf hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 2: Trage das Volumen des Kegelstumpfes ein. Runde auf eine Nachkommastelle.
Der Kegelstumpf hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 3: Trage das Volumen des jeweiligen quadratischen Pyramidenstumpfes ein. Runde auf eine Nachkommastelle.
| a) | a1 = cm; a2 = cm; h = cm V = cm³ |
| b) | a1 = cm; a2 = cm; h = cm V = cm³ |
| c) | AG = cm²; AD = cm²; h = cm V = cm³ |
| d) | AG = cm²; AD = cm²; h = cm V = cm³ |
| AG: Grundfläche; AD: Deckfläche | |
richtig: 0falsch: 0
Aufgabe 4: Trage die Höhe des quadratischen Pyramidenstumpfes ein. Runde auf ganze Zentimeter.
| a) | V = cm³; a1 = cm; a2 = cm h = cm |
| b) | V = cm³ a1 = cm; a2 = cm h = cm |
richtig: 0falsch: 0
Aufgabe 5: Trage die fehlenden Werte der Kegelstümpfe ein. Runde das Volumen (a) auf eine Nachkommastelle und die Höhe (b) auf ganze Zentimeter.
| a) | r1 = cm; r2 = cm; h = cm V = cm³ |
| b) | r1 = cm; r2 = cm; V = cm³ h = cm |
richtig: 0falsch: 0
Aufgabe 6: Ein quadratischer Pyramidenstumpf hat die unten angegebenen Maße. Trage die Länge der Seite a1 ein (Satz des Pythagoras).
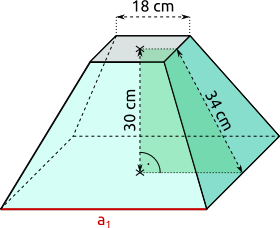
Die Seite a1 hat eine Länge von cm.
Versuche: 0
Aufgabe 7: Ein quadratischer Pyramidenstumpf hat die unten angegebenen Maße. Trage seine Höhe ein (Satz des Pythagoras).
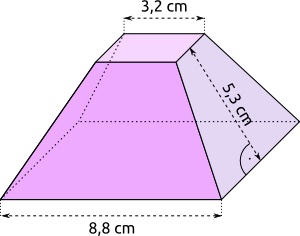
Die Höhe des Stumpfes beträgt cm.
Versuche: 0
Aufgabe 8: Ein quadratischer Pyramidenstumpf hat die unten angegebenen Maße. Trage seine Höhe ein (Satz des Pythagoras).
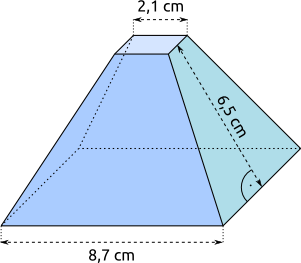
Die Höhe des Stumpfes beträgt cm.
Versuche: 0
Aufgabe 9: Ein Kegelstumpf hat die unten angegebenen Maße. Trage seine Höhe ein (Satz des Pythagoras).
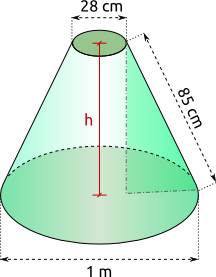
Die Höhe des Stumpfes beträgt cm.
Versuche: 0
Aufgabe 10: Trage das Höhe des Kegelstumpfes ein. Runde auf ganze Zentimeter (Satz des Pythagoras).
Die Höhe des Stumpfes beträgt cm.
richtig: 0falsch: 0
Aufgabe 11: Ein Kegelstumpf hat die unten angegebenen Maße. Trage die Länge der Seitenkante ein (Satz des Pythagoras).
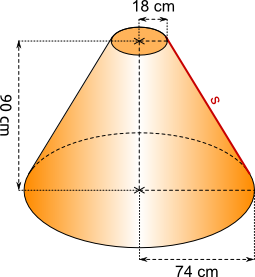
Die Länge der Seitenkante beträgt cm.
Versuche: 0
Aufgabe 12: Trage die Länge der Seitenlinie des Kegelstumpfes (s) ein. Runde auf eine Stelle nach dem Komma (Satz des Pythagoras).
Die Seitenlinie (s) ist cm lang.
Runde auf eine Nachkommastelle.
richtig: 0falsch: 0
Aufgabe 13: Trage das Höhe des Kegelstumpfes ein. Runde auf ganze Zentimeter (Trigonometrie).
Die Höhe des Stumpfes beträgt cm.
richtig: 0falsch: 0
Aufgabe 14: Trage die Höhe des Kegelstumpfes ein. Runde auf ganze Zentimeter (Trigonometrie).
Die Höhe des Stumpfes beträgt cm.
richtig: 0falsch: 0
Aufgabe 15 |
a) Wie viel Flüssigkeit passt insgesamt in das untere Glas? |
a) Insgesamt passen ,5 cm3 Flüssigkeit ins Glas.
b) Es befinden sich ,8 cm3 Orangensaft im Glas.
Versuche: 0
Aufgabe 16: Das folgende Trinkglas hat einen Bodendurchmesser von (d1), einen Öffnungsdurchmesser von (d2) und eine Glashöhe von (h1). Der Hohlraum des Glases ist bis zu einer Höhe von (h2) mit Wasser gefüllt. Wie viel Wasser befindet sich im Glas? Trage den ganzzahligen Wert ein.
Im Glas befinden sich cm3 Wasser.
richtig: 0falsch: 0
Aufgabe 17: Ein quadratischer Pyramidenstumpf hat die Maße: a2 = cm, h = cm und V = cm³. Wie lang ist seine Grundkante (a1)?
Antwort: Die Grundkannte ist cm lang.
richtig: 0falsch: 0
Trigonometrische Berechnungen an quadratischen Pyramidenstümpfen
a) Das Trapez der schrägen Seitenfläche | |||||||||||||
 |
|
||||||||||||
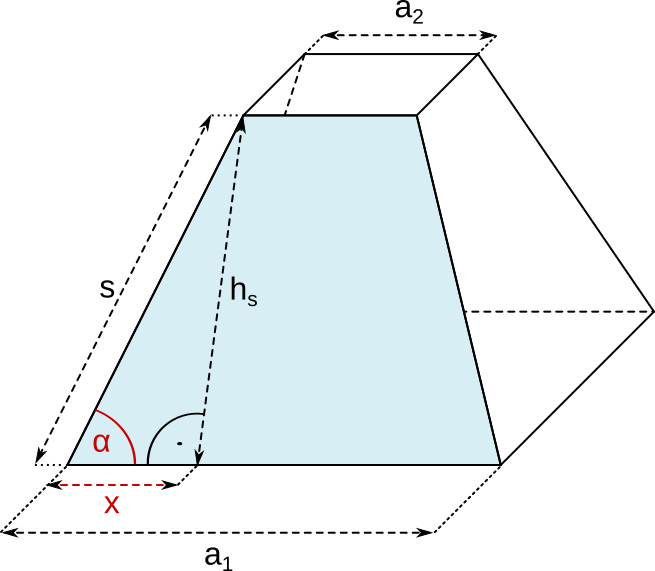b) Das Trapez des senkrechten, frontalen Querschnitts. | |||||||||||||
 |
|
||||||||||||
c) Das Trapez des senkrechten, diagonalen Querschnitts. | |||||||||||||
 |
|
||||||||||||
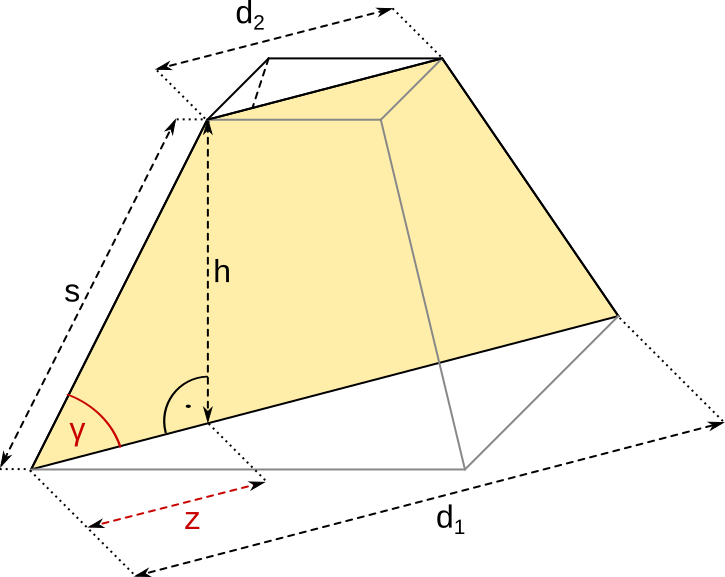Aufgabe 18: Trage in die Tabelle die fehlenden Werte des quadratischen Pyramidenstumpfes ein. Runde auf eine Nachkommastelle. Verwende beim Weiterrechnen jedoch alle Nachkommastellen.
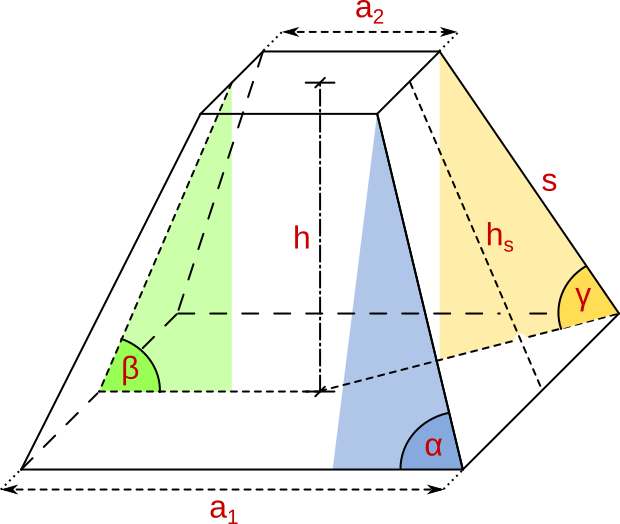
| a) | a1 | a2 | h | hs | s | α | β | γ |
| ° | ° | ° |
Angaben in cm
richtig: 0falsch: 0
| b) | a1 | a2 | h | hs | s | α | β | γ |
| ° | ° | ° |
Angaben in cm
richtig: 0falsch: 0
Aufgabe 19: Trage in die Tabelle die fehlenden ganzzahligen Werte des quadratischen Pyramidenstumpfes ein. Verwende beim Rechnen alle Nachkommastellen.
| a) | a1 | a2 | h | hs | s | α | β | γ |
| , | ,0 | , | ,° | ,° |
Angaben in cm | Der β-Grad-Wert ist gerundet.
richtig: 0falsch: 0
| b) | a1 | a2 | h | hs | s | α | β | γ |
| , | , | ,° | ,° | ,° |
Angaben in cm
richtig: 0falsch: 0