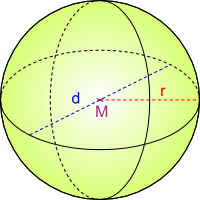
Kugel
Die Kugel ist ein Körper, bei dem jeder Punkt der Oberfläche gleich weit vom Körpermittelpunkt entfernt ist.
Aufgabe 1: Trage die ganzzahligen Werte der Ergebnisse unten ein.
Formeln:- r = Radius; d = Durchmesser; M = Mittelpunkt
- Volumen: V = 4 3 · π · r3
- Oberfläche: O = 4 · π · r2
- r = 4 cm
- Volumen: V = 4 3 · π · (4 cm)3 = ,08 cm³
- Oberfläche: O = 4 · π · (4 cm)2 = ,06 cm²
Versuche: 0
Aufgabe 2: Klick das richtige Volumen und die richtige Oberfläche an.
|
a) Oberfläche = cm²
richtig: 0 | falsch: 0
|
||
|
b) Volumen = cm³
richtig: 0 | falsch: 0
|
||
Aufgabe 3: Trage die fehlenden ganzzahligen Werte ein. (Die aufgeführten Kommastellen sind gerundet.)
| Radius r | cm | dm | m | m |
| Durchmesser d | cm | dm | m | m |
| Volumen V | cm³ | dm³ | m³ | m³ |
| Oberfläche O | cm² | dm² | m² | m² |
richtig: 0falsch 0
Aufgabe 4: Wie schwer ist eine Granitkugel mit einem Durchmesser von 25 cm? 1 cm³ Granit wiegt 2,8 g. Runde auf eine Stelle nach dem Komma.
Die Kugel wiegt kg.
richtig: 0falsch: 0
Aufgabe 5: Elsa bestellt sich 4 Eiskugeln mit einem Durchmesser von 5 cm. Wie viel Milliliter Eis erhält sie? Runde auf ganze Milliliter.

Elsa erhält ml Eis.
Versuche: 0
Aufgabe 6: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein. Auchte auf die Maßeinheit.
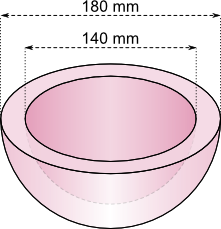
V = ,44 cm³; O = ,35 cm²
Versuche: 0
Aufgabe 7: Die halbkugelförmige Kuppel einer Kapelle soll neu gestrichen werden. Sie hat einen Umfang von 22 m. Wie viel Quadratmeter Decke sind zu streichen. Trage den fehlenden ganzzahligen Wert ein.
Es sind , m² Decke zu streichen.
richtig: 0falsch: 0
Aufgabe 8: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein.

V = ,85 cm³; O = ,47 cm²
Versuche: 0
Aufgabe 9: Eine Kugel hat eine Oberfläche von 1995 cm². Wie groß ist ihr Durchmesser? Trage den fehlenden ganzzahligen Wert ein.
Der Durchmesser beträgt , cm.
richtig: 0falsch: 0
Aufgabe 10: Eine Kugel hat ein Volumen von . Trage unten die Oberfläche der Halbkugel ein, die den gleichen Umfang hat wie die Kugel. Runde das Ergebnis auf ganze Quadratzentimeter.
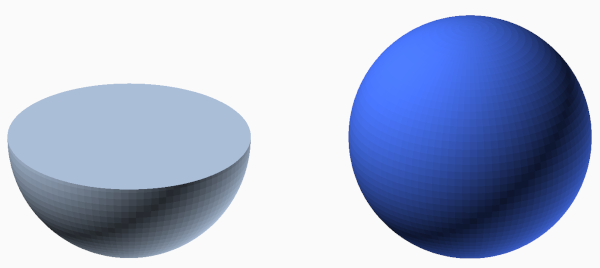
OHalbkugel = cm²
richtig: 0falsch: 0
Aufgabe 11: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein.
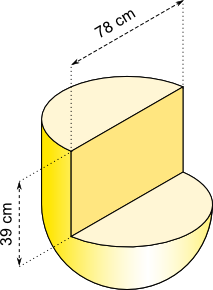
V = ,49 cm³; O = ,45 cm²
Versuche: 0
Aufgabe 12: Zwei Kugeln haben jeweils einen Durchmesser von 15 cm. Die eine ist aus Stahl (Dichte 7,85 g/cm³), die andere aus Polystyrol (Dichte 1,05 g/cm³). Wie groß ist der Gewichtsunterschied zwischen diesen beiden Kugeln? Runde auf zehntel kg.
Die Stahlkugel wiegt kg mehr als die Polystyrolkugel.
Versuche: 0
Aufgabe 13: Die Halbkugel und der Kegel haben denselben Durchmesser (d) von und dasselbe Volumen. Trage unten die Höhe des Kegels ein.
h = cm
richtig: 0falsch: 0
Aufgabe 14: Trage die fehlenden ganzzahligen Werte für Volumen und Oberfläche des folgenden Körpers ein.
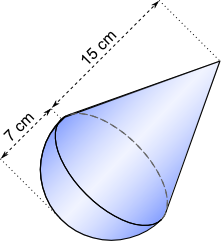
V = ,07 cm³; O = ,89 cm²
Versuche: 0
Aufgabe 15: Berechne Volumen und Oberflächeninhalt des folgenden Körpers. Der Radius des kleinen, kugelförmigen Bereichs in der Mitte beträgt 5 cm. Der Radius des großen, umliegenden, kugelförmigen Bereichs beträgt 10 cm. Die gelben Flächen stehen in einem 90° Winkel zueinander. Ihre geraden Kanten peilen genau den Mittelpunkt an. Runde auf eine Nachkommastelle.
| O = cm²
|
V = cm³
|
Aufgabe 16: Die orange Halbkugel hat ein Volumen von . Die Höhe des blauen Zylinders beträgt die doppelte Länge des Halbkugelradius. Wie groß ist die Mantelfläche des Zylinders? Trage den fehlenden ganzzahligen Wert ein.
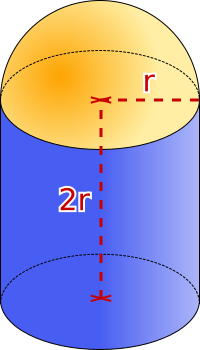
Die Mantelfläche des Zylinders beträgt , cm2
richtig: 0falsch: 0
Aufgabe 17: Von einer Kugel, die genau 1072 g wiegt, wird behauptet, dass sie aus Silber sei. Silber hat eine Dichte von 10,49 g/cm³. Welchen Durchmesser müsste diese Kugel haben, sollte sie tatsächlich aus Silber sein. Runde auf eine Stelle nach dem Komma.
Eine echte Silberkugel hätte einen Durchmesser von cm.
Versuche: 0
Aufgabe 18: Die untere Hälfte eines kugelförmigen Aquariums hat einen Rauminhalt von 39 Litern. Welchen Innendurchmesser hat das Glas an dieser Stelle, an der sich das Wasser am weitesten ausbreitet? Runde auf ganze Zentimeter.
 |
Das Glas hat an dieser Stelle einen Innendurchmesser von cm.
Versuche: 0
Aufgabe 19: In einen Zylinder mit einem Innendurchmesser von 9,6 cm wird eine Stahlkugel gelegt. Der Wasserpegel steigt um 2,7 cm. Welchen Durchmesser hat die Kugel? Runde auf eine Nachkommastelle.

nicht maßstabsgetreu
Die Kugel hat einen Durchmesser von cm.
Versuche: 0
Aufgabe 20: Ein Fußball hat einen Durchmesser von 22 cm. Wieviel cm2 Leder werden benötigt, wenn bei der Produktion mit einem Verschnitt von 17 % gerechnet wird. Runde auf ganze cm2.
Für jeden Ball werden dann cm2 Leder berechnet.
Versuche: 0
Aufgabe 21: Eine Kugel ist innen hohl. Ihr äußerer Radius beträgt und der innere .
| a) | Welches Volumen hat die Wandung? Runde auf ganze Kubikzentimeter. |
| b) | Aus wie viel Prozent des Gesamtvolumens besteht die Wandung? Runde auf ganze Prozent. |
| a) | Die Wandung hat ein Volumen von cm3. |
| b) | Sie nimmt % des Gesamtvolumens ein. |
richtig: 0falsch: 0
Aufgabe 22: Aus einem 6 mm dicken Tropfen (kugelförmig) ist eine Seifenblase mit einem Durchmesser von 12 cm entstanden. Welche Wandstärke hat die Seifenblase? Runde auf 4 Nachkommastellen.
 |
Die Wand der Seifenblase ist mm dick.
Versuche: 0
Aufgabe 23: Eine ein Kilogramm schwere Kugel besteht aus einem Material, das g/cm3 wiegt. Welchen Durchmesser hat diese Kugel? Runde auf eine Nachkommastelle.
Die Kugel hat einen Durchmesser von cm.
richtig: 0falsch: 0
Aufgabe 24: Berechne a) das Volumen und b) den Oberflächeninhalt des folgenden aus einer Halbkugel, einem Zylinder und einem Kegel zusammengesetzten Körpers. Die eingezeichneten Strecken haben die unten aufgeführten Größen. Runde das Ergebnis auf ganze Kubik- und Quadratzentimeter.
a = | b = | c = | d =
| a) V = cm³ | b) O = cm² | |
|
|
Aufgabe 25: Berechne a) das Volumen und b) den Oberflächeninhalt des folgenden Körpers mit a = cm. Trage den jeweils fehlenden ganzzahligen Wert ein.
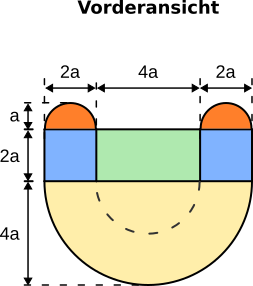 |
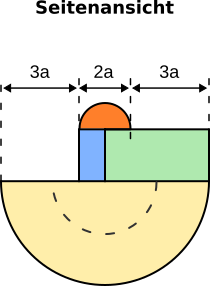 |
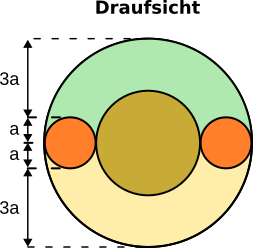 |
|
| V = cm³
|
O = cm²
|
Aufgabe 26: Am Äquator hat die Erde einen Radius von 6371 km. Berechne den Umfang des 52,5ten Breitenkreis, auf dem Berlin liegt. Runde auf ganze Kilometer.

Der Umfang des 52,5ten Breitenkreis beträgt km.
Versuche: 0
Aufgabe 27: Ein Weißer Zwerg ist ein kleiner, sehr kompakter alter Stern. Es gibt im Universum welche, die haben die Masse unserer Sonne, etwa 2 Quadrilliarden Tonnen. Das ist ungefähr das 333 000-fache unserer Erdmasse. Während unsere Sonne jedoch einen Radius von rund 700 000 km aufweist, haben manche Weiße Zwerge nur den anderthalbfachen Radius der Erde. Wenn man von diesen Daten ausgeht: Wie viel mal größer ist die Dichte eines solchen Weißen Zwergs im Vergleich zur Dichte der Erde? Trage die fehlende ganze Zahl ein.

| Dichte = | Masse |
| Volumen |
Die Dichte eines solchen Weißen Zwergs ist ,7 Mal so groß wie die Dichte der Erde.
Versuche: 0
Aufgabe 28: Die Erde hat eine Dichte von durchschnittlich 5,5 g/cm3. Welche Masse hätte eine Billardkugel mit einem Durchmesser von 57,2 mm, wenn sie aus der Materie eines Weißen Zwerges (Aufgabe oben) bestände.

Masse = Dichte · Volumen
Eine Billardkugel hätte eine Masse von ,5 kg.
Versuche: 0