Prismen ergründen
Prismen untersuchen
Prismen sind Körper, bei denen die Grundfläche und die Deckfläche
- Vielecke,
- deckungsgleich und
- zueinander parallel sind.
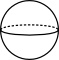
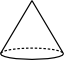
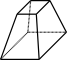
Aufgabe 1: Ordne die Körper richtig zu.
| Prismen |  |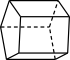
 |
 |
 |
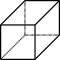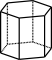| keine Prismen |  |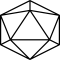
 |
 |
 |
Aufgabe 2: Trage unten die richtigen Zahlen ein.
Aufgabe 3: Schiebe die unteren Terme (n+2; 2n; 3n) in die richtige Spalte.
| Grundfläche am Prisma |
Anzahl
am Prisma |
||
| Ecken | Kanten | Flächen | |
| Dreieck | 6 () | 9() | 5() |
| Viereck | 8() | 12() | 6() |
| Fünfeck | 10() | 15() | 7() |
| Sechseck | 12() | 18() | 8() |
| Siebeneck | 14() | 21() | 9() |
| Achteck | 16() | 24() | 10() |
| n-Eck | 2n | 3n | n+2 |
Aufgabe 4: Klick unten die Figuren an, die die Seitenfläche eines Prismas bilden können.
(!Achteck) (!Dreieck) (!Kreis) (Parallelogramm) (Quadrat) (Raute) (Rechteck) (!Trapez)
Prismen konstruieren
Aufgabe 5: Ziehe die orangen Punkte so, dass 2 Quadernetze entstehen. Wenn die Netze richtig konstruiert sind, färben sie sich blau.
Aufgabe 6: Ergänze die Flächen mit dem Füllwerkzeug (
) ab den Punkten mit jeweils einem Rechteck so, dass ein Würfelnetz ensteht. Wenn alles richtig ist, erscheint die Meldung: "Aufgabe erledigt".
Erzeugt mit Z.u.L.
Aufgabe 7: Ziehe die roten Punkte so, dass 6 Prismen entstehen. Die Punkte für das nachfolgende Prisma werden freigegeben, sobald das davorliegende Prisma richtig konstruiert ist. Nach Fertigstellung des letzten Prismas ist nur noch ein roter Punkt zu sehen.
Java Runtime notwendig
Aufgabe 8: Beim untere Prismennetz fehlt die dreieckige Grund- und Deckfläche. Konstruiere mit Hilfe der aufgeführten Werkzeuge zuerst die fehlenden Eckpunkte. Erstelle dann die Grund- und die Deckfläche mit dem Füllwerkzeug (). Wenn alles richtig ist, erscheint eine Erfolgsmeldung.
Erzeugt mit Z.u.L.
Aufgabe 9: Erzeuge mit dem Füllwerkzeug () die rote Fläche des Prismennetzes an den Punkten A und B. Die Konstruktionslinien der gegenüberliegenden Fläche helfen dir bei der Lösung. Wenn alles richtig ist, erscheint eine Erfolgsmeldung.
Erzeugt mit Z.u.L.