Prisma 
- Prismen erkennen und konstruieren (A 1 - A 22)
- Formeln (A 23 - A 27)
- Rechteckprisma (Quader) (A 28 - A 31)
- Parallelogrammprisma (A 32 - A 34)
- Dreieckprisma (A 35 - A 38)
- Trapezprisma (A 39 - A 43)
- Gemischte Aufgaben (A 44 - A 58)
Prismen sind Körper, bei denen die Grundfläche und die Deckfläche
|
 |
Anmerkung: Volumen und Oberflächeninhalt von Prisma und Zylinder werden faktisch nach gleichem Schema berechnet. Im Film wird in didaktischer Vereinfachung der Zylinder als Spezialfall eines Prismas mit unendlich vielen Ecken eingeordnet. Streng mathematisch gesehen ist ein Zylinder aber kein Prisma, da die Grundfläche eines Zylinders kein Polygon mit unendlich vielen Ecken sondern ein Kreis ohne Ecken ist.
![]()
Aufgabe 1: Ziehe an den Gleitern und verändere so die beiden Prismen. Wenn du beim oberen Prisma den roten Punkt verschiebst, steht die Grundfläche (blau) nicht mehr senkrecht zur Deckfläche (grün). Da beide Flächen aber immer noch Vielecke, deckungsgleich und parallel zueinander sind, bleibt der Körper ein Prisma.
Aufgabe 2: Ordne zu, ob es sich beim entsprechenden Körper um ein Prisma handelt oder nicht.
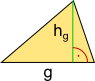
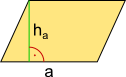
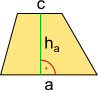
Aufgabe 3: Unten siehst du 4 Flächen die u.a. die Grundfläche eines Prismas bilden können. Ordne die Bezeichnungen und die Formen richtig zu.
 |
 |
 |
 |
Versuche: 0
Aufgabe 4: Gerade Prismen können ganz unterschiedliche Grund- und Deckflächen haben. Die Mantelfläche besteht jedoch immer aus so vielen Rechtecken, wie die Grundfläche Seiten hat. (Bei schiefen Prismen bestehen die Mantelflächen aus Parallelogrammen.) Trage unten ein, aus wie vielen Rechtecken die Mantelfläche des jeweiligen geraden Prismas besteht.
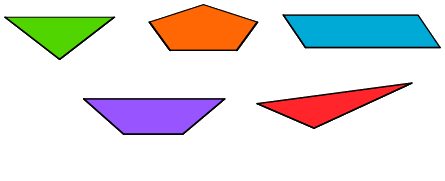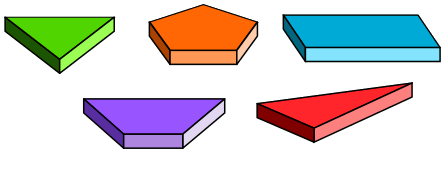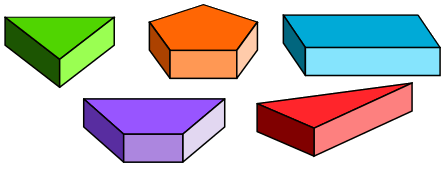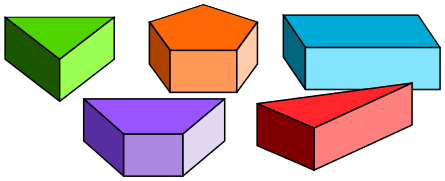
Anzahl der Rechtecke, aus denen die Mantelfläche des jeweiligen geraden Prismas besteht.
A: ; B: ; C: ; D: ; E:
Versuche: 0
Aufgabe 5: Gib an, wie viel Ecken, Kanten und Flächen das jeweilige Prisma besitzt.
| Grundfläche am Prisma |
Anzahl
am Prisma |
||||
| Ecken | Kanten | Flächen | E + F - K = | ||
| Dreieck | |||||
| Viereck | |||||
| Fünfeck | |||||
| Sechseck | |||||
| Siebeneck | |||||
| Achteck | |||||
| n-Eck | |||||
Versuche: 0
Aufgabe 6: Klick an, welcher Körper mit dem jeweiligen Netz gebildet werden kann.
Aufgabe 7: Markiere nur die Aussagen, die zu einem Prisma passen.
| Ein Dreiecksprisma hat 9 Kanten. | |
| Jedes Prisma hat 6 Flächen. | |
| Es gibt Prismen mit 5 Flächen. | |
| Die Grund- und Deckfläche eines Prismas sind immer Vielecke. | |
| Ein Quader ist kein Prisma. | |
| Die Grund- und die Deckfläche eines Prismas haben die gleiche Form und Größe. | |
| Ein Zylinder ist auch ein Prisma. | |
| Ein Prisma ist eine Fläche. |
Versuche: 0
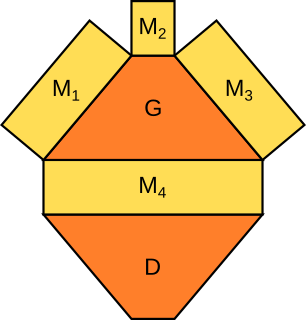
Aufgabe 8: Das grüne Dreieck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Bandnetz dieses Prismas entsteht. Fange mit Punkt A an und verändere dann den jeweils folgenden Punkt.
richtig: 0 | falsch: 0
Aufgabe 9: Das grüne Dreieck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren drei Gleiter verschoben werden. Das rote Kreuz markiert die Prismenhöhe.
richtig: 0 | falsch: 0
Aufgabe 10: Das grüne Dreieck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren drei Gleiter verschoben werden. Das rote Kreuz markiert die Prismenhöhe.
richtig: 0 | falsch: 0
Aufgabe 11: Das grüne Viereck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren drei Gleiter verschoben werden. Das rote Kreuz markiert die Prismenhöhe.
richtig: 0 | falsch: 0
Aufgabe 12: Das grüne Rechteck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters mit einer Höhe von entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden.
richtig: 0 | falsch: 0
Aufgabe 13: Das grüne Trapez bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters mit einer Höhe von entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden.
richtig: 0 | falsch: 0
Aufgabe 14: Das grüne Viereck bildet die Grundfläche eines Prismas. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters mit einer Höhe von entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden.
richtig: 0 | falsch: 0
Aufgabe 15: Das grüne Trapez bildet die Grundfläche eines Prismas. Das Prisma liegt auf einem Rechteck der Mantelfläche. Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren drei Gleiter verschoben werden. Das rote Kreuz markiert die Prismenhöhe.
richtig: 0 | falsch: 0
Aufgabe 16: Das grüne Dreieck bildet die Grundfläche eines Prismas. Das Prisma liegt auf einem Rechteck der Mantelfläche. Seine hier schräg nach hinten verlaufende Höhe beträgt . Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren drei Gleiter verschoben werden. Achtung: In der Kavalierperspektive werden die nach hinten führenden Strecken mit halber Länge gezeichnet.
richtig: 0 | falsch: 0
Aufgabe 17: Das grüne Rechteck bildet die Grundfläche eines Prismas (Quaders). Das Prisma liegt auf einem Rechteck der Mantelfläche. Seine hier schräg nach hinten verlaufende Höhe beträgt . Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden. Achtung: In der Kavalierperspektive werden die nach hinten führenden Strecken mit halber Länge gezeichnet.
richtig: 0 | falsch: 0
Aufgabe 18: Das grüne Parallelogramm bildet die Grundfläche eines Prismas. Das Prisma liegt auf einem Rechteck der Mantelfläche. Seine hier schräg nach hinten verlaufende Höhe beträgt . Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden. Achtung: In der Kavalierperspektive werden die nach hinten führenden Strecken mit halber Länge gezeichnet.
richtig: 0 | falsch: 0
Aufgabe 19: Das grüne Trapez bildet die Grundfläche eines Prismas. Das Prisma liegt auf einem Rechteck der Mantelfläche. Seine hier schräg nach hinten verlaufende Höhe beträgt . Alle orangen Gleiter sind so zu verschieben, bis das Schrägbild eines Prismengitters entsteht. Die Punkte mit gleichem Buchstaben sind übereinanderzulegen. Zuerst sollten die unteren vier Gleiter verschoben werden. Achtung: In der Kavalierperspektive werden die nach hinten führenden Strecken mit halber Länge gezeichnet.
richtig: 0 | falsch: 0
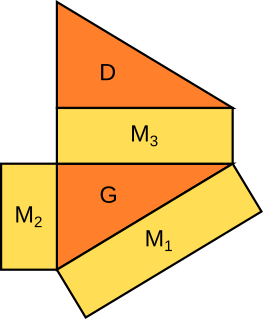
Aufgabe 20: Ordne die Buchstaben der Volumengröße der Prismen nach. Links ist der Buchstabe des kleinsten, rechts der Buchstabe des größten Prismas.
klein , , , , groß
Versuche: 0
Aufgabe 21: Klick unten die richtigen Antworten zu den Prismen der Grafik an.
|
a) Prisma A hat ein größeres Volumen als jeder andere Körper: richtig falsch b) Folgende Körper haben das gleiche Volumen wie Prisma A: B C D c) Prisma C und D können so verändert werden, dass das Volumen von Prisma C größer ist als das von Prisma D: richtig falsch d) Wenn nur die Höhe (blau) der Prismen halbiert wird, halbiert sich auch der Rauminhalt folgender Prismen: A B C D e) Wenn die Höhe (blau) und die Tiefe (grün) der Prismen halbiert wird, dann ist das neue Volumen ein so groß wie das alte Volumen. f) Das Volumen von Prisma B ist halb so groß wie das Volumen von Prisma: A C D g) Das Volumen von Prisma A, B, und D wird 27 Mal größer, wenn die Höhe, die Breite und die Tiefe dieser Prismen jeweils Mal größer wird. |
Versuche: 0
Aufgabe 22: Klick unten die Figuren an, die die Seitenfläche eines Prismas bilden können.
Achteck Dreieck Kreis Parallelogramm Quadrat Raute Rechteck Trapez
Versuche: 0
Aufgabe 23: Ordne jede Formel zur Flächenberechnung einer anderen Fläche zu.
 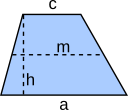 |
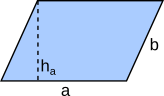 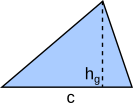 |
Aufgabe 24: Klick die richtigen Terme an.
Formeln:
|
Versuche: 0
Aufgabe 25: Berechne mit der richtigen Formel aus Aufgabe 24 die Volumen der beiden Prismen im Kopf.
a) |
b) |
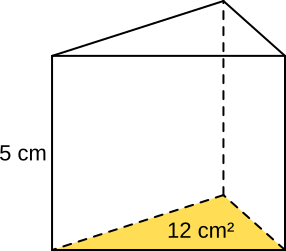 |
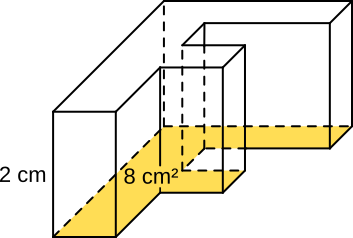 |
V = cm³ |
V = cm³ |
Versuche: 0
Aufgabe 26: Berechne mit der richtigen Formel aus Aufgabe 24 die Oberfläche der beiden Prismen im Kopf.
a) |
b) |
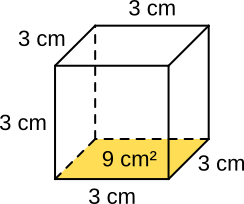 |
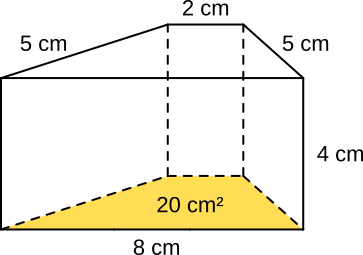 |
O = cm² |
O = cm² |
Versuche: 0
Aufgabe 27: Berechne den Oberflächeninhalt (O) des Prismas aus dem Netz unten.
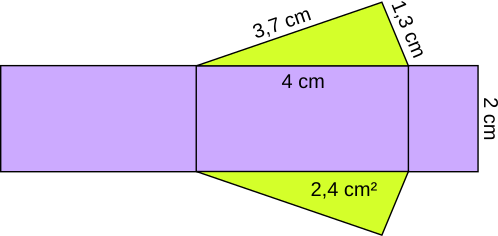
O = cm²
Versuche: 0
Rechteckprisma (Quader)
 |
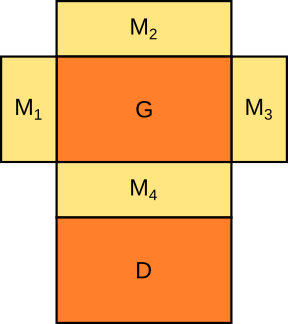 |
V = G · h | O = 2G + u · h
G = Grundfläche | u = Grundflächenumfang | h = Prismenhöhe
| Aufgabe 28: | a) Trage das Volumen des Quaders ein. |
| b) Trage die Oberfläche des Quaders ein. |
Angaben in cm
|
a) V = cm³
|
b) O = cm²
|
Aufgabe 29: Das untere Rechteck ist die Grundfläche eines Prismas mit einer Höhe von cm.
| a) Trage das Volumen des Prismas ein. | |
| b) Trage die Oberfläche des Prismas ein. |
|
a) V = cm3
|
b) O = cm2
|
Aufgabe 30: Ein Ei wird in das Wasser eines Quaders mit einer quadratischen, 5 cm langen Grundfläche (innen) gelegt. Das Wasser steigt danach um 2,8 cm. Welches Volumen hat das Ei?
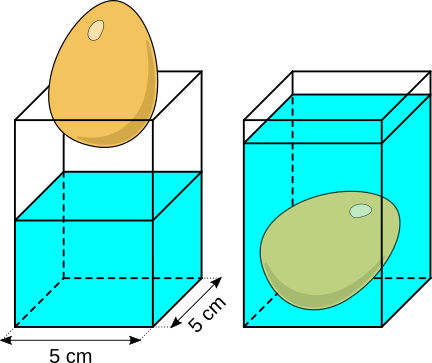
Das Ei hat ein Volumen von ml.
Versuche: 0
Aufgabe 31: Ein Quader hat ein Volumen von m3. Er ist und . Wie ist er?
Der Quader ist m .
richtig: 0falsch: 0
Parallelogrammprisma
 |
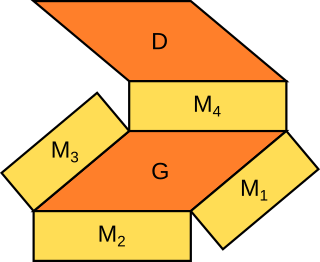 |
V = G · h | O = 2G + u · h
G = Grundfläche | u = Grundflächenumfang | h = Prismenhöhe
| Aufgabe 32: | a) Trage das Volumen des Parallelogrammprismas ein. |
| b) Trage die Oberfläche des Parallelogrammprismas ein. |
Angaben in cm
|
a) V = cm³
|
b) O = cm²
|
Aufgabe 33: Das untere Parallelogramm ist die Grundfläche eines Prismas mit einer Höhe von cm.
| a) Trage das Volumen des Prismas ein. | |
| b) Trage die Oberfläche des Prismas ein. |
|
a) V = cm3
|
b) O = cm2
|
Aufgabe 34: Berechne den fehlenden Wert des Parallelogrammprismas.
| Volumen | V = dm3 | |
| dm |
richtig: 0falsch: 0
| Aufgabe 35: | a) Trage das Volumen des Dreieckprismas ein. |
| b) Trage die Oberfläche des Dreieckprismas ein. |
Angaben in cm
|
a) V = cm³
|
b) O = cm²
|
Aufgabe 36: Das Dreieck ist die Grundfläche eines Prismas. Es hat die Maße a = cm, b = cm, c = cm und hc = cm. Das Prisma hat eine Höhe von cm.
| a) Trage das Volumen des Prismas ein. | |
| b) Trage die Oberfläche des Prismas ein. |
|
a) V = cm3
|
b) O = cm2
|
Aufgabe 37: Die roten Kanten des Würfels sind 10 cm lang. Welches Volumen hat der gesamte grüne Bereich in diesem Würfel?
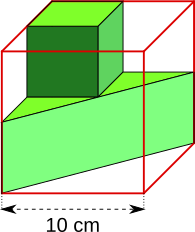
Das Volumen beträgt cm3.
Versuche: 0
Aufgabe 38: Berechne den fehlenden Wert des Dreieckprismas.
| Volumen | V = dm3 | |
| dm |
richtig: 0falsch: 0
| Aufgabe 39: | a) Trage das Volumen des Trapezprismas ein. |
| b) Trage die Oberfläche des Trapezprismas ein. |
Angaben in cm
|
V = cm³
|
O = cm²
|
Aufgabe 40: Ein Trapez ist die Grundfläche eines Prismas. Es hat die Maße a = cm, b = cm, c = cm, d = cm und ha = cm. Das Prisma hat eine Höhe von cm.
| a) Trage das Volumen des Prismas ein. | |
| b) Trage die Oberfläche des Prismas ein. |
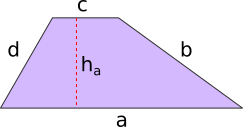
Die Zeichnung ist nicht maßstabsgetreu.
|
a) V = cm3
|
b) O = cm2
|
Aufgabe 41: Trage die Höhe des Prismas ein.
| Volumen | V = cm3 | |
| Trapezhöhe | ha = cm | |
| Trapezseite | a = cm | |
| Trapezseite | c = cm | |
| Prismahöhe | h = cm |
richtig: 0falsch: 0
Aufgabe 42: Trage die Länge der Trapezseite c ein.
| Volumen | V = cm3 | |
| Prismahöhe | h = cm | |
| Trapezhöhe | ha = cm | |
| Trapezseite | a = cm | |
| Trapezseite | c = cm |
richtig: 0falsch: 0
Aufgabe 43: Trage die fehlenden Größen für die Prismen ein.
| Grundfläche G | cm² | ||
| Körperhöhe h | cm | ||
| Volumen V | cm³ | ||
richtig: 0falsch: 0 |
|||
Aufgabe 44: Die inwändige Grundfläche eines 2 hohen Wasserbeckens ist ein Quadrat mit einer Seitenlänge von 18. Das Becken wird zu ¾ mit Wasser gefüllt. Wie viel m³ Wasser befinden sich im Becken?
Es befinden sich m³ Wasser im Aquarium.
richtig: 0falsch: 0
Aufgabe 45: Die Grafik zeigt die Grundflächen verschiedener Prismen. Sie sind alle 8 cm hoch. Trage das entsprechende Volumen ein.
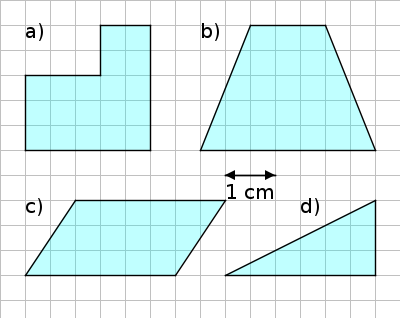
Va = cm³ Vb = cm³ Vc = cm³ Vd = cm³
Versuche: 0
Aufgabe 46: Die untere 5 cm hohe Kuchenform ist ein Prisma. Seine Grundfläche hat die Form einer Rakete. Welches Volumen hat die Form?
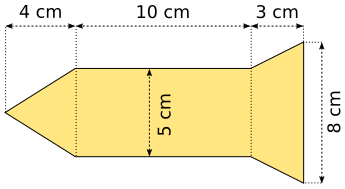
Die Kuchenform hat ein Volumen von cm³.
Versuche: 0
Aufgabe 47: Der folgende Körper besteht aus einer Quader und einem Dreiecksprisma. Trage das Volumen ein.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 48: Das folgende Prisma besteht aus einer Quader mit quadratischer Grundfläche und einem Trapezprisma. Trage das Volumen ein. Runde es auf eine Nachkommastelle.
Das Prisma hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 49: Berechne Oberfläche und Volumen des Prismas.
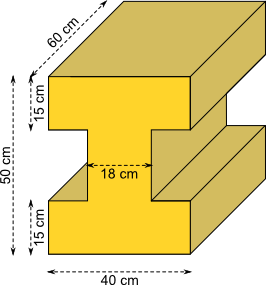
|
Die Oberfläche beträgt dm². Das Volumen beträgt dm³. |
Versuche: 0
Aufgabe 50: Welches Gewicht hat die abgebildete Steintreppe, wenn das verwendete Mamor eine Dichte von 2,7 g/cm³ hat? Runde auf eine Stelle nach dem Komma.
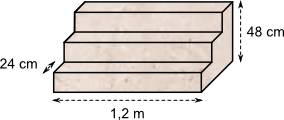
Die Treppe wiegt kg.
Versuche: 0
Aufgabe 51: Trage das Volumen des folgenden Prismas ein.
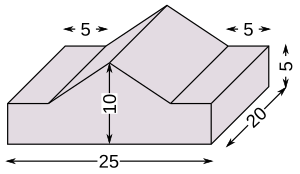
Maße in cm
Das Prisma hat ein Volumen von cm3.
Versuche: 0
Aufgabe 52: Trage das Volumen des folgenden Prismas ein.
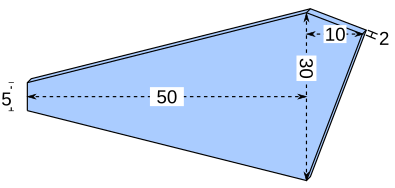
Angaben in cm
V = cm³
Versuche: 0
Aufgabe 53: Das untere Werkstück ist aus Stahl. Stahl hat eine Dichte von 7,9 g/cm³. Das Stahlprisma wiegt g. Die Seite a ist cm und die Seite b cm lang. Welche Höhe (ha) hat die dreieckige Grundfläche des Prismas?
Das Dreieck hat über der Seite a eine Höhe von cm.
richtig: 0falsch: 0
Aufgabe 54: Berechne Volumen und Oberfläche eines Prismas mit folgendem gleichschenkligem Dreieck als Grundfläche und einer Körperhöhe von Körperhöhe: 0 cm. Berechne die fehlende Seitenlänge mit Hilfe des Satzes von Pythagoras.
| a) Trage das Volumen des Prismas ein. Runde auf eine Stelle nach dem Komma. | |
| b) Trage die Oberfläche des Prismas ein. Runde auf eine Stelle nach dem Komma. |
|
a) V = cm³
|
b) O = cm²
|
Aufgabe 55: Berechne Volumen und Oberfläche eines Prismas mit folgendem gleichschenkligem Trapez als Grundfläche und einer Körperhöhe von Körperhöhe: 0 cm. Berechne die fehlende Seitenlänge mit Hilfe des Satzes von Pythagoras.
| a) Trage das Volumen des Prismas ein. Runde auf eine Stelle nach dem Komma. | |
| b) Trage die Oberfläche des Prismas ein. Runde auf eine Stelle nach dem Komma. |
|
a) V = cm³
|
b) O = cm²
|
Aufgabe 56: Eine 140 cm hohe Marmorsäule besitzt die Grundfläche eines regelmäßigen Sechsecks mit einer Seitenlänge von 30 cm. Marmor hat eine Dichte von 2,7 g/cm³. Wie schwer ist die Säule? Runde auf ganze Kilogramm.
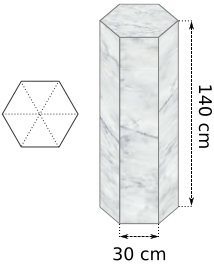
Die Säule wiegt kg.
Versuche: 0
Aufgabe 57: Die grüne Klappe verdeckt die quadratische Öffnung eines Prismas. Die Öffnung dahinter hat eine Fläche von . Trage unten das Hohlraumvolumen des regelmäßigen Sechseckprismas ein. Runde auf ganze Kubikzentimeter.
V = cm³
richtig: 0falsch: 0
Aufgabe 58: Ein Rasengitterstein aus Leichtbeton ist 60 cm lang, 40 cm breit und 8 cm tief. Er wiegt 31,74 kg. Der Beton hat eine Dichte von 2,3 g/cm3. Welche Länge hat eine Seite der quadratischen Hohlräume?
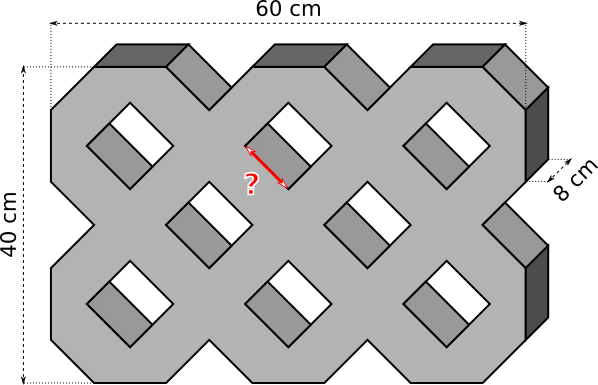
Die quadratischen Hohlräume haben eine Länge von cm.
Versuche: 0