Potenz 
Aufgabe 1: Trage die richtigen Begriffe ein.
- Eine (pultiMiklation) gleicher Zahlen kann vereinfacht geschrieben werden; aus 2 · 2 · 2 wird 23.
- Die große Grundzahl nennt man (saBis) und die hochgestellte kleine Zahl (nExopent).
- Die Basis tritt so oft als (tokFar) auf, wie es der Exponent angibt.
- Basis und Exponent bilden die (toPenz) (23). Das Ergebnis ist der (zwettenPor) (8).
- Beispiel:
Versuche: 0
Aufgabe 2: Trage in die Textfelder die richtigen Fachbegriffe ein.
Versuche: 0
Aufgabe 3: Trage die richtige Faktoren und Ergebnisse ein.
| a) 23 = · · = | b) 43 = · · = | |
| c) 25 = · · · · = | d) 52 = · = | |
| e) 53 = · · = | f) 102 = · = | |
| g) 104 = · · · = | h) 14 = · · · = |
Versuche: 0
Aufgabe 4: Schreibe als Produkt aus gleichen Faktoren. Verwende als Mal-Zeichen den Stern (*) oder das X.
Beispiel: 23 = 2 * 2 * 2
=
richtig: 0falsch: 0
Aufgabe 5: Trage das richtige Ergebnis ein.
=
richtig: 0falsch: 0
Aufgabe 6: Trage die richtige Basis und den richtigen Exponenten ein.
| a) x = | b) x = |
| c) x = | d) x = |
richtig: 0falsch: 0
Aufgabe 7: Ergänze die Tabelle.
| a) | b) | c) | d) | |
| Potenz | 01 | 23 | ||
| Basis | 4 | 5 | ||
| Exponent | 6 | 7 |
richtig: 0falsch: 0
Besondere Potenzen
Jede Potenz mit dem Exponenten 0 ergibt den Wert 1:
10 = 1; 70 = 1; 100 = 1; 1750 = 1 ...Jede Potenz mit dem Exponenten 1 hat denselben Wert wie ihre Basis:
11 = 1; 71 = 7; 101 = 10; 1751 = 175 ...
Aufgabe 8: Ordne die Terme richtig zu.
| a) 35 = | b) 53 = |
| c) 3 · 5 = | d) 5 · 3 = |
| e) = = | |
3 + 3 + 3 + 3 + 3 (3 + 3 + 3) + (3 + 3 + 3) + (3 + 3 + 3) 3 · 3 · 3 3 · 3 · 3 · 3 · 3 33 5 + 5 + 5 5 · 5 · 5
Versuche: 0
Aufgabe 9:
Trage unten die richtigen Ergebnisse ein. Verwechsle nicht Potenzen 24 → (2 · 2 · 2 · 2) mit Produkten 2 · 4 → (4 + 4).
| Potenzen |
Achtung
←≠→ |
Produkte | ||
| a) 22 = | b) 32 = | a') 2 · 2 = | b') 3 · 2 = | |
| c) 23 = | d) 33 = | c') 2 · 3 = | d') 3 · 3 = | |
| e) 24 = | f) 34 = | e') 2 · 4 = | f') 3 · 4 = | |
| g) 25 = | h) 35 = | g') 2 · 5 = | h') 3 · 5 = | |
Versuche: 0
Aufgabe 10: Trage die richtigen Werte ein.
| a) = | b) |
1 | 2 | = | ||
| 2 | ||||||
| c) = | d) = | |||||
richtig: 0falsch: 0
Aufgabe 11: Setze <, > oder = richtig ein.
| a) 23 32 | b) 34 43 | c) 52 25 |
| d) 24 42 | e) 30 40 | f) 53 35 |
Versuche: 0
Aufgabe 12: Trage den kleinstmöglichen Exponenten ein.
|
a) 2 > 8 b) 2 > 8 c) 2 < 8 |
richtig: 0falsch: 0
Aufgabe 13: Trage die richtigen Werte ein.
a) 64 = 8 = 3 = 2 b) 81 = 9 = 4
Versuche: 0
Aufgabe 14: Trage die richtigen Exponenten ein.
|
Versuche: 0
Aufgabe 15: Trage die richtigen Exponenten ein.
a) = b) =
richtig: 0falsch: 0
Aufgabe 16: Gib die fehlenden Werte an.
| a) |
|
||||||||||||
| b) |
|
||||||||||||
| c) |
|
||||||||||||
richtig: 0falsch: 0
Aufgabe 17: Trage die richtigen Ergebnisse unten ein. Achte auf die Rechenregeln.
| a) = | b) = |
| c) = | d) = |
| e) = | f) = |
| g) = | h) = |
richtig: 0falsch: 0
Aufgabe 18 Trage die richtigen Ergebnisse unten ein. Achte auf die Rechenregeln.
|
a) (66 - 54)2 + (37-33)2 =
b) (42 - 39)3 · (87 - 85)5 = c) (23 - 25)4 - (23 - 32) = |
Versuche: 0
Aufgabe 19: Die folgende Figur ist aus kleinen, gleich großen Würfeln zusammengesetzt. Der kleine grüne Würfel hat eine Kantenlänge von . Wie groß ist das Volumen des gesamten Körpers?


















Der gesamte Körper hat ein Volumen von cm3.
richtig: 0falsch: 0
Aufgabe 20: Die Fläche des Körpernetzes besteht aus gleich großen Quadraten. Jede Quadratseite (a) ist 7 cm lang. Welches Volumen hat der an den grauen Klebelaschen zusammengeklebte Körper?
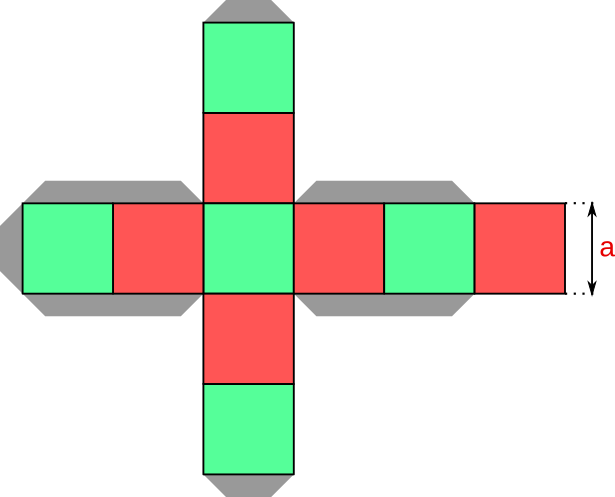
Der Körper hat ein Volumen von cm3.
Versuche: 0
Aufgabe 21: Die folgende Figur ist aus kleinen, gleich großen Würfeln zusammengesetzt. Ein kleiner Würfel hat eine Kantenlänge von . Trage das Volumen der gesamten Figur ein.
Die gesamte Figur hat ein Volumen von cm3.
richtig: 0falsch: 0
Aufgabe 22: Trage die fehlenden Werte der gesuchten Terme ein. Beachte die Klammern in Term d).
|
a) Die Fläche des Quadrates = b) Das Volumen des Würfels = c) Das Volumen der zwei Würfel = d) Das Volumen der acht Würfel = () |
Versuche: 0
Aufgabe 23: Jonas baut mit kleinen Steckwürfeln einen großen Würfel. Für eine Stange benötigt er fünf Würfel. Fünf Stangen nebeneinander bilden eine Schicht. Aus fünf solcher Schichten besteht der große Würfel.
a) Gib die Potenz an, mit der der
große Würfel berechnet werden kann. Antwort:
b) Aus wie vielen kleinen Würfeln besteht der große Würfel?
Antwort: Aus
kleinen Würfeln.
Versuche: 0
Aufgabe 24: Zu Weihnachten bestellt eine Drogerie Geschenkpackungen mit Seifen. Sie ordert deshalb 10 Kartons. In jedem Karton befinden sich drei Schachteln mit je drei Geschenkpackungen. Jede Packung enthält drei verschiedene Seifen.
a) Wie viele einzelne Seifen befinden sich in
den 10 Kartons? Antwort:
Seifen
b) Wie viele Geschenkpackungen hat die Drogerie noch, wenn
54 verkauft wurden? Antwort:
Geschenkpackungen
Versuche: 0
Aufgabe 25: Ein Gärtner möchte 100 Blumensträuße auf dem Wochenmarkt verkaufen. Er bindet immer fünf Blumen zu einem Strauß zusammen und jeweils fünf Sträuße wickelt er in Cellophan ein. Fünf solcher Bündel stellt er in einen Eimer.
a) Wie viele Eimer benötigt er? Antwort:
Eimer
b) Wie viele Blumen muss er schneiden? Antwort:
Blumen
Versuche: 0
Aufgabe 26: Herr Grohe möchte sein quadratisches Bad mit einer Seitenlänge von 1,64 m Metern mit Fliesen auskleiden. Jede Fliese misst 20 cm · 20 cm.
| a) | Wie groß ist zu Fläche des Bades in dm2? Antwort: dm2 |  |
| b) | Welche Fläche hat eine einzelne Fliese in dm2? Antwort: dm2 | |
| c) | Die Fliesen sollen so verlegt werden, dass zwischen ihnen eine Fuge mit 5 mm Breite entsteht. Welche Fläche ist unter diesen Voraussetzungen rein rechnerisch für das Setzen einer Fliese plus ihres Fugenanteils in dm2 zu berücksichtigen? Antwort: dm2 | |
| d) | Wie viele Fliesen muss Herr Grohe kaufen, wenn die Fugenbreite an allen Wänden nur 2,5 mm beträgt? Antwort: Fliesen. |
Versuche: 0
Aufgabe 27: Drei Seerosen in einem Teich wachsen so, dass sie sich ihre Menge täglich verdoppelt. Wie viele Seerosen befinden sich nach einer Woche im Teich?
Nach einer Woche befinden sich Seerosen im Teich.
Versuche: 0
Aufgabe 28: Es gibt Bakterien, die teilen sich jede Stunde auf. Aus einer alten entstehen zwei neue Bakterien. Wie viele Bakterien, die sich aus dem ersten Bakterium entwickelt haben, existieren nach einem Tag?
0h
Nach einem Tag existieren Bakterien.
Versuche: 0
Aufgabe 29: Die "Kochsche Schneeflocke" besteht anfangs aus einem gleichseitigen Dreieck. Dann wird jede Strecke gedrittelt und über dem Mittelstück ein neues gleichseitiges Dreieck gebildet. Mit jedem Schritt vervierfachen sich die Kanten der Schneeflocke. Wie viele Kanten hat die Flocke nach n Schritten?
Antwort: Nach n Schritten hat die Schneeflocke · Kanten.
Versuche: 0
Aufgabe 30: Deine Eltern und deine Großeltern sind deine Vorfahren. Wie viele Vorfahren hattest du insgesamt bis zu deinen Urururururgroßeltern?
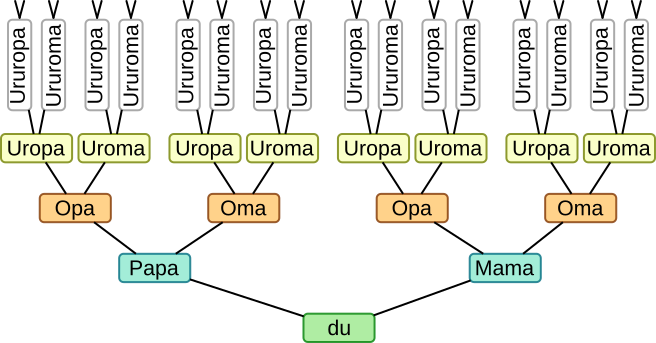
Insgesamt sind es Personen.
Versuche: 0
Aufgabe 31: Vorausgesetzt, eine Generation umfasst 25 Jahre, dann hat vor 500 Jahren die 20. Generation vor dir gelebt. Aus wie vielen Vorfahren bestand vor ca. 500 Jahren die 20. Generation vor dir?
Diese Generation bestand aus Personen.
Versuche: 0
Aufgabe 32: Klick an, was aus dir geworden wäre, wenn ein einziger deiner Abermillionen Vorfahren einen anderen Partner gewählt hätte.
 |
Bist du eine göttliche Fügung oder ein darwinistischer Zufall?
Aufgabe 33: Ein Science-Fiction-Liebhaber entdeckt um 12.00 Uhr eine "VIPER MARK 2" am Himmel. Um 12.15 Uhr erhalten 20 Personen von ihm diese Nachricht per Smartphone. Um 12.30 Uhr sendet jeder von ihnen diese Information an 20 andere Personen. Diese übermitteln die Nachricht ebenfalls nach 15 Minuten an jeweils 20 unterschiedliche Personen u.s.w. Wie viele Menschen wissen um 13.05 Uhr von diesem Ereignis, wenn jeder genau 20 Freunde informierte?

|
|
Um 13.05 Uhr wissen Menschen darüber Bescheid, dass die Viper gesichtet wurde.
Versuche: 0


