Statistiken auswerten 
- Statistische Kenngrößen (A 1 - A 9)
- Relative Häufigkeit (A 10 - A 23)
- Quartilen (A 24 - A 28)
- Boxplot (A 29 - A 32)
In Statistiken werden große Zahlenmengen planmäßig erfasst, untersucht und dargestellt.
Aufgabe 1: Schüler einer achten Klasse wurden danach befragt, wie viele Stunden sie in der Wochen im Internet verbringen. Die unterschiedlichen Antworten kannst du der Liste entnehmen. Trage unten die richtigen Werte ein.
| Mädchen (M) | Jungen (J) | |
| Internetstunden pro Woche |
0, 2, 3, 4, 4, 4, 5, 5, 6, 7, 7, 8, 10, 12 | 5, 4, 20, 8, 15, 7, 4, 9, 14, 8, 5, 2, 5, 3, 1, 2 |
| Wie viele Schüler gehen gar nicht ins Internet? | |
| M: | J: |
| Wie viele Schüler sind über 5 Stunden im Internet? | |
| M: | J: |
| Wie viele Schüler sind über 10 Stunden im Internet? | |
| M: | J: |
| Wie viele Schüler wurden insgesamt befragt? | |
| M: | J: |
| Trage den Durchschnitt des Internetbesuchs der Schüler ein. | |
| M: h/w | J: h/w |
| Klick an, welche Auflistung übersichtlicher ist: | |
Versuche: 0
Aufgabe 2: Die folgenden Begriffe haben in Statistiken eine große Bedeutung. Ziehe sie an die richtige Stelle.
| Die ist die ungeordnete Liste dieser Daten. | → 4, 9, 2 | |||
| Die ist die von der kleinsten zur größten Zahl geordnete Urliste. | → 2, 4, 9 | |||
| Der (Median) ist der Wert in der Mitte der Rangliste. | → 2, 4, 9 | |||
| Die ist der Unterschied zwischen größtem () und kleinstem () Wert. | → 9 - 2 = 7 | |||
Der
berechnet sich aus der Summe der Listenwerte durch deren Anzahl.
|
→ (2 + 4 + 9) : 3 = 5 | |||
| Der Mittelwert wird auch als arithmetische Mittel oder als Durchschnitt bezeichnet. | ||||
Versuche: 0
Aufgabe 3:
|
a) Wandle die Urliste (Zahlmarkierung durch Anklicken) in eine Rangliste um.
|
richtig: 0falsch: 0
Hat die Rangliste eine gerade Anzahl von Daten, dann steht kein Wert genau in der Mitte. Der Zentralwert wird dann aus dem Mittelwert der beiden Daten gebildet, die der Mitte am nächsten stehen.
Beispiel: Rangliste(2,4,6,8) → Zentralwert = (4 + 6) : 2 = 5
Aufgabe 4:
|
a) Wandle die Urliste (Zahlmarkierung durch Anklicken) in eine Rangliste um.
|
richtig: 0falsch: 0
Aufgabe 5:
|
a) Wandle die Urliste (Zahlmarkierung durch Anklicken) in eine Rangliste um.
|
richtig: 0falsch: 0
Aufgabe 6: Trage in die untere Tabelle den fehlenden Wert ein, durch dessen Hinzufügung erst der gültige Mittelwert zustande kommt.
| A | B | C | D | E | Mittelwert A-E |
richtig: 0falsch: 0
Aufgabe 7: Trage den fehlenden Mittelwert ein: In der Firma Reifen-Radke werden monatlich folgende Gehälter ausgezahlt:
| Paul Grünling | Auszubildender | 600 € |
| Çalışkan Okur | KFZ-Mechaniker | 1 800 € |
| Anette Scholz | Einzelhandelskauffrau | 1 900 € |
| Leo Meinauer | KFZ-Meister | 2 800 € |
| Ewald Radke | Firmeninhaber | 6900 € |
|
Ewald Radke behauptet: "Das Durchschnittseinkommen in meinem Betrieb beträgt €. |
Versuche: 0
Aufgabe 8: Trage im Text die fehlenden Werte ein.
Angler Pedro Hail erstellt sich ein Diagramm seiner kapitalen Fänge. Vor Freunden behauptet er korrekt: "Meine Fische haben im Durchschnitt eine Länge von cm." Beim Betrachten des Diagramms entgegnet sein Angelbruder, dass hier der Zentralwert von cm viel aussagekräftiger sei. Wem gibst du recht?
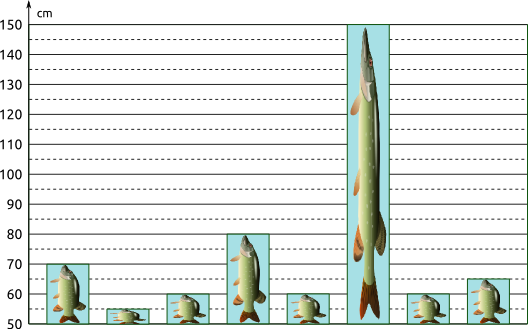
Versuche: 0
Aufgabe 9: Sabine bekommt 18 € Taschengeld. Ihre Klasse hat eine Taschengeldliste der Schüler angefertigt und dabei folgende Ergebnisse erlangt:
14 €, 19 €, 22 €, 20 €, 14 €, 105 €, 12 €, 18 €, 22 €, 14 €,
14 €, 12 €, 0 €, 20 €, 16 €,
14 €. Sabine nimmt diese Liste als Grundlage, um mit ihrem Vater neu über ihr Taschengeld zu verhandeln. Sie deutet an, dass der Durchschnittswert dieser Liste ein angemessenes Taschengeld wäre. Der Vater meint, dass das Maximum (105 €) und das Minimum (0 €) der Urliste gestrichen werden müssten. Den Durchschnitt dieser neuen Liste könnte er sich sehr gut als künftiges Taschengeld vorstellen. Was wird Sabine zum Angebot ihres Vaters sagen? Trage die gesuchten Werte unten ein.
| gewünschte Werte der Tochter |
akzeptierte Werte des Vaters |
|
| Maximum | € | € |
| Minimum | € | € |
| Spannweite | € | € |
| Durchschnitt | € | € |
Versuche: 0
Aufgabe 10: Trage unten die richtigen Werte ein.
In zwei achten Klassen stellen sich jeweils drei Schüler und Schülerinnen zur Klassensprecher-Wahl. Die Auszählung aller Stimmen ergibt folgendes Ergebnis.
| Klasse | Schüler | Stimmen |
| 8a | Murat | 15 |
| Anna | 8 | |
| Joel | 2 | |
| 8b | Eva | 15 |
| Gina | 6 | |
| Dennis | 3 | |
Murat behauptet anschließen, er habe genauso viele Stimmen erhalten wie Eva. Die widerspricht und meint, sie habe mehr Stimmen erhalten. Gina erklärt: "Absolut gesehen habt ihr gleich abgeschnitten, denn jeder von euch hat Stimmen erhalten. In Murats Klasse sind aber mehr Schüler als in Evas. Die 8a hat Schüler und in der 8b sind es . Bei einem fairen Vergleich müsst ihr eure erhaltenen Stimmen durch die Anzahl der Schüler eurer Klasse teilen."
| Murat rechnet | : = |
| Eva rechnet | : = |
So gesehen hat Eva einen größeren Stimmenanteil.
Versuche: 0
Die relative Häufigkeit gibt einen prozentualen Anteil wieder. Sie wird genutzt, um unterschiedliche Größen miteinander zu vergleichen.
| Relative Häufigkeit = | absolute Häufigkeit |
| Gesamtzahl |
Eine siebte Klasse besteht aus 10 Jungen und 15 Mädchen. Die relative Häufigkeit der Jungen in dieser Klasse wird dann folgendermaßen berechnet:
| Relative Häufigkeit = | Anzahl der Jungen | = | 2 | = 0,4 = 40% |
| Anzahl aller Schüler | 5 |
Aufgabe 11: Gib die richtigen Daten an.
| Klasse | 7 | 8 | 9 | |||||||
| Jungen | Anzahl | 10 | 12 | 9 | ||||||
| Relative Häufigkeit |
Bruch |
|
|
|
||||||
| Dezimal | 0,4 | |||||||||
| Prozent | 40 % | % | % | |||||||
| Mädchen | Anzahl | 15 | 9 | 15 | ||||||
| Relative Häufigkeit |
Bruch |
|
|
|
||||||
| Dezimal | 0,6 | |||||||||
| Prozent | 60 % | % | % | |||||||
| Alle Schüler | Anzahl | 25 | 21 | 24 | ||||||
|
gesehen sind in Klasse 7 und 9 gleich viele Mädchen. gesehen sind in Klasse 7 weniger Mädchen als in Klasse 9. |
Versuche: 0
Aufgabe 12: Klick unten etwa 20 Mal auf die Münze und trage ein, mit welcher relative Häufigkeit das Wappen erscheint. Runde auf die vorgegebenen Nachkommastellen.
|
|
|||
| Anzahl | relative Häufigkeit |
||
Kopf |
0 | 0,000 = 0,0 % | |
Wappen |
0 | 0,000 = 0,0 % | |
| Summe: | 0 | ||
Aufgabe 13: Klick unten etwa 50 Mal auf den Würfel und trage dann die relative Häufigkeit der gewürfelten Augenzahlen ein. Runde auf die vorgegebenen Nachkommastellen.
|
|
|||
| Anzahl | relative Häufigkeit | ||
|
|
0 | 0,000 = 0,0 % | |
| 0 | 0,000 = 0,0 % | ||
| 0 | 0,000 = 0,0 % | ||
| 0 | 0,000 = 0,0 % | ||
| 0 | 0,000 = 0,0 % | ||
| 0 | 0,000 = 0,0 % | ||
| Summe: | 0 | ||
Aufgabe 14: |
Folgende Ergebnisse einer Klassenarbeit werden an die Tafel geschrieben. Gib |
|||||||||||||||
|
||||||||||||||||
a) Die relative Häufigkeit der Note 3 ist %. |
Versuche: 0
Aufgabe 15: Klick die relativen Häufigkeiten in der richtigen Reihenfolge der Größe nach an.
Versuche: 0
Aufgabe 16: Das Diagramm zeigt, wie viele Eier 2016 in welcher Haltungsform produziert wurden. Trage die relative Häufigkeit der jeweiligen Haltungsform als Dezimalzahl ein. Runde auf zwei Nachkommastellen.
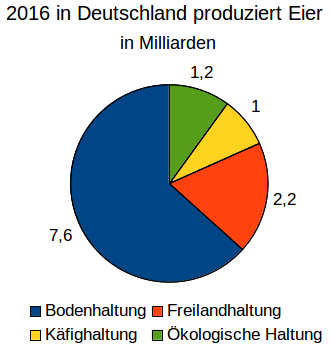
| Haltungsart | relative Häufigkeit |
| Boden | |
| Freiland | |
| Käfig | |
| Ökologisch |
auf zwei Nachkommastellen gerundet
Versuche: 0
Aufgabe 17: In einer Schule wurde ermittelt, wie viele Schüler je Klassenstufe Mitglied in einem Sportverein sind. Folgende Ergebnisse kamen dabei heraus. Trage die relative Häufigkeit als Dezimalzahl auf zwei Nachkommastellen genau ein und finde heraus, welche Stufe die "sportlichste" ist.
| Klassen- stufe |
Schüler | im Verein |
relative Häufigkeit |
| 5 | 48 | 26 | |
| 6 | 40 | 22 | |
| 7 | 42 | 24 | |
| 8 | 52 | 27 | |
| 9 | 38 | 19 | |
| 10 | 33 | 16 |
Relativ betrachtet, gehen die meisten Schüler aus Jahrgangsstufe in einen Sportverein.
richtig: 0falsch: 0
Aufgabe 18: Beim Basketballtraining übten Murat, Jenny, Hanna, Michael und Ulf den Ball in den Korb zu werfen. Die Ergebnisse wurden aufgeschrieben. Trage die relative Häufigkeit als Prozentangabe in die Tabelle ein. Runde auf eine Nachkommastelle. Wer konnte am besten Körbe werfen?
| Würfe | Treffer | relative Häufigkeit |
|
| Murat | 48 | 26 | % |
| Jenny | 40 | 22 | % |
| Hanna | 42 | 24 | % |
| Michael | 52 | 27 | % |
| Ulf | 38 | 19 | % |
Das beste Wurfergebnis erzielte .
richtig: 0 | falsch: 0
Aufgabe 19: In einem Landkreis wurden Jugendliche befragt, was ihnen wichtig ist. Trage die absolute Häufigkeit der Antworten in die Tabelle ein.
Umfrageteilnehmer:
| Jugendzentrum | Spielplätze | Mediathek | |
| relative Häufigkeit | |||
| absolute Häufigkeit |
richtig: 0falsch: 0
Aufgabe 20: In einer Boutique wurden trendige T-Shirts in folgenden Größen und Mengen verkauft. Da das T-Shirt gut ankommt, bestellt die Abteilung anteilmäßig 200 T-Shirts des Nachfolgermodells. Trage die relative Häufigkeit der bisher verkauften T-Shirts ein. Gib an, welche Größe wie oft nachbestellt werden sollte.
 |
| Größe | XS | S | M | L | XL | XXL |
| Bisherige Menge | 9 | 18 | 36 | 54 | 45 | 18 |
| Relative Häufigkeit | % | % | % | % | % | % |
| Nachbestellung | ||||||
Versuche: 0
Aufgabe 21: Zu einem länderübergreifenden Schüleraustausch treffen sich Schüler aus folgenden Städten in Stuttgart.
| Stadt | Schüler- anzahl |
| Augsburg | 9 |
| Basel | 5 |
| Bern | 7 |
| Innsbruck | 1 |
| München | 7 |
| Salzburg | 4 |
| Stuttgart | 12 |
| Wien | 3 |
| Zürich | 2 |
Trage die absoluten und die relativen Häufigkeiten den teilnehmenden Länder ein.
| Herkunftsland | absolute Häufigkeit |
relative Häufigkeit |
| Deutschland | ||
| Österreich | ||
| Schweiz |
Versuche: 0
Aufgabe 22: Bei einer Wahlumfrage in Bamberg werden 400 Personen befragt, davon geben 208 an, Partei A zu wählen. In Berlin geben 750 Personen Auskunft. Dort werden 345 Personen Partei A ihre Stimme geben. Absolut betrachtet, sind in Berlin 137 Personen mehr für Partei A als in Bamberg. Wie sieht das Verhältnis aber bei einer relativen Betrachtung aus? Gib an, wie viel Prozent der Befragten in den jeweiligen Städten Partei A wählen.
|
Versuche: 0
Aufgabe 23: Die Automobilindustrie erwartet von ihren Zulieferern, dass von einer Million ausgelieferter Teile maximal 20 fehlerhaft sein dürfen. Die Firma "Schob" erhält vom Automobilhersteller "WV" den Auftrag, 150 Tage lang jeden Tag 1 000 Kontrollleuchten anzuliefern. Wie viele dieser Leuchten dürfen nach der angegebenen Vorgabe fehlerhaft sein?
Von allen ausgelieferten Leuchten dürfen defekt sein.
Versuche: 0
Quartilen
Das untere Quartil Qu halbiert die untere Hälfte, das obere Quartil Qo die obere Hälfte einer Rangliste. Der Unterschied zwischen dem oberen und unteren Quartil heißt Quartilenabstand (Qo - Qu). Da sich nicht jede Datenmenge in vier exakt gleich große Teilabschnitte zergliedern lässt, werden die beiden Quartilen mit unterschiedlichen Verfahren verortet. Hier werden zwei vorgestellt, die zu je leicht abweichenden Ergebnissen führen können.
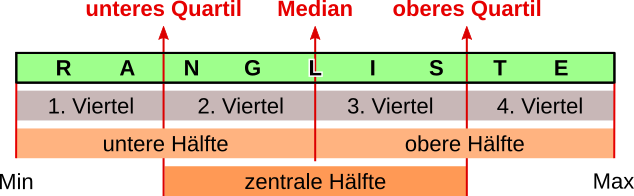
Quartilen durch Median vom Median ermitteln
Der Median teilt die Datenmenge in zwei Hälften. Die Daten links vom Median gehören zur unteren Datenhälfte und die Daten rechts vom Median gehören zur oberen Datenhälfte. Besteht eine Rangliste aus einer geraden Anzahl von Daten, dann ist der Median das arithmetische Mittel ø aus dem größten Wert der unteren Hälfte und dem kleinsten Wert der oberen Hälfte. Das untere Quartil halbiert dementsprechend die untere Datenhälfte vor dem Median und das obere Quartil die obere Datenhälfte nach dem Median.
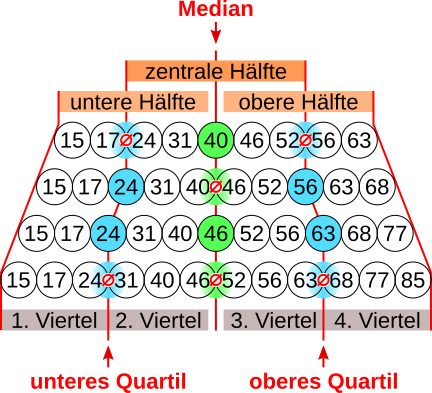
Aufgabe 24: Gib die aufgeführten Kenngrößen der folgenden Rangliste an. Nutze den Median vom Median um das jeweilige Quartil zu bestimmen.
| Minimum: | unteres Quartil: | ||
| Maximum: | oberes Quartil: | ||
| Median: | Quartilenabstand: | ||
richtig: 0falsch: 0 |
|||
Aufgabe 25: Gib die aufgeführten Kenngrößen der folgenden Häufigkeitsliste an. Nutze den Median vom Median um das jeweilige Quartil zu bestimmen.
| Minimum: | unteres Quartil: | ||
| Maximum: | oberes Quartil: | ||
| Median: | Quartilenabstand: | ||
richtig: 0falsch: 0 |
|||
Quartilen durch Vierteln der Rangliste ermitteln
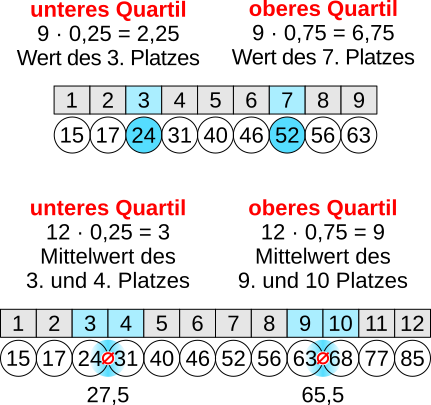
Für die Bestimmung des unteren Quartils wird die Anzahl der Rangplätze mit 0,25 (¼), für das obere Quartil mit 0,75 (¾) multipliziert. Ist das Ergebnis eine Kommazahl, legt der Datenwert des folgenden Rangplatzes das jeweilige Quartil fest. Ist das Ergebnis eine ganze Zahl, ist das jeweilige Quartil das arithmetische Mittel aus dem Datenwert des berechneten und des darauf folgenden Rangplatzes.
Aufgabe 26: Gib die aufgeführten Kenngrößen der folgenden Rangliste an. Nutze die geviertelte Ranglistenposition um das jeweilige Quartil zu bestimmen.
| Minimum: | unteres Quartil: | ||
| Maximum: | oberes Quartil: | ||
| Median: | Quartilenabstand: | ||
|
richtig: 0falsch: 0 |
|||
Aufgabe 27: Gib die aufgeführten Kenngrößen der folgenden Häufigkeitsliste an. Nutze die geviertelte Ranglistenposition um das jeweilige Quartil zu bestimmen.
| Minimum: | unteres Quartil: | ||
| Maximum: | oberes Quartil: | ||
| Median: | Quartilenabstand: | ||
richtig: 0falsch: 0 |
|||
Aufgabe 28: Trage in das untere Textfeld 6 bis 20 Werte einer Rangliste ein. Lass dir die entsprechenden Kenndaten ausgeben. Die Quartilen können unterschiedlich sein bei Ranglisten mit 9, 13, 17 ... Elementen. Also immer dann, wenn der Quotient aus der Elementenanzahl und 4 einen Rest von 1 ergibt (Bsp. 9 : 4 = 2 Rest 1 | 13 : 4 = 3 Rest 1 ).
Rangliste (Trennzeichen:
)
Quartilen durch Median vom Median
Quartilen durch Vierteln der Rangliste
Boxplot
Ein Boxplot ist hilfreich für die Übersicht von großen Datenmengen. Mit ihm werden Minimum, unteres Quartil, Medium, oberes Quartil und Maximum grafisch dargestellt. Manchmal wird auch der Mittelwert mit angezeigt. Die Werte zwischen unterem und oberem Quartil (zentrale Hälfte) werden als Box dargestellt. Eine Linien verbinden die Box mit dem Minimum und eine mit dem Maximum. Diese beiden Linien werden Antennen (Whisker) genannt.
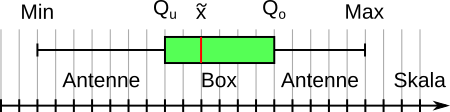
Aufgabe 29: Lies die richtigen Werte aus dem Boxplot ab und trage sie unten ein.
| Min | Qu | Qo | Max | |
richtig: 0falsch: 0
Aufgabe 30: Ziehe die Elemente der Grafik so, dass zu den gegebenen Kennwerten ein gültiger Boxplot entsteht. Ziehe in folgender Reihenfolge: Min, Max, Qu, Qo, ![]() .
.
| Min | Qu | Qo | Max | |
richtig: 0 | falsch: 0
Aufgabe 31: Ziehe die Elemente der Grafik so, das zu den gegebenen Kennwerten ein gültiger Boxplot entsteht. Ziehe in folgender Reihenfolge: Min, Max, Qu, Qo, ![]() .
.
richtig: 0 | falsch: 0
Aufgabe 32: In der Klasse wird eine Spontanerhebung gemacht. Jeder Schüler legt seine mitgebrachten Buntstifte auf den Tisch und zählt sie ab. An der Tafel wird folgendes Ergebnis festgehalten. Trage die richtigen Werte in die Tabelle ein und ziehe die Elemente der Grafik so, dass zu den gegebenen Kennwerten ein gültiger Boxplot entsteht. Ziehe in folgender Reihenfolge: Min, Max, Qu, Qo, ![]() .
.
Anzahl der Buntstifte je Schüler
|
| Min | Qu | Qo | Max | |
richtig: 0falsch: 0



