Proportionale Zuordnung 
| Proportional a) | Je mehr, desto mehr. |
b) | Je weniger, desto weniger. |
Proportionale Zuordnungen geben gleichmäßiges Wachstum an. Verdoppelt, verdreifacht oder halbiert sich eine Größe, dann verdoppelt, verdreifacht oder halbiert sich auch die ihr zugeordnete Größe (2 Teile: 1 € → 4 Teile: 2 €). Der Quotient proportionaler Wertepaare ist immer gleich groß.
| x | 1 | = 0,5 | 2 | = 0,5 | 4 | = 0,5 |
| y | 2 | 4 | 8 |
Aufgabe 1: Bei einem Flugzeug mit gleichbleibender Geschwindigkeit bilden Zeit und Strecke eine proportionale Zuordnung. In doppelter Zeit wird die doppelte Strecke zurückgelegt. Die Koordinaten stehen auf einer Linie. Bewege in der Grafik den orangen Gleiter und beobachte, was passiert.
Aufgabe 2: Entnimm der oberen Grafik die Strecke, die das Flugzeug nach den aufgeführten Zeiten zurücklegt. Mit dem orangen Gleiter kannst du das Flugzeug bewegen. Trage die Ergebnisse in die Tabelle ein.
| Stunden (h) | 1 | 2 | 3 | 4 | 5 |
| Kilometer (km) |
Versuche: 0
Aufgabe 3: In Aufgabe a ist y doppelt so groß wie x, in Aufgabe b dreifach so groß wie x und in c halb so groß wie x. Trage die richtigen Werte ein.
| a) | b) | c) | |||||
| y = 2x | y = 3x | y = ½x | |||||
| x | y | x | y | x | y | ||
| 1 | 2 | 1 | 3 | 2 | 1 | ||
| 2 | 2 | 4 | |||||
| 3 | 3 | 6 | |||||
| 4 | 4 | 8 | |||||
| 5 | 5 | 12 | |||||
Versuche: 0
Aufgabe 4: Ordne unten die Zuordnungen richtig ein: Sind sie proportional oder nicht?
Aufgabe 5: Ordne die Tabellen unten richtig ein: Geben sie proportionale Verhältnisse wieder (z.B. doppelte Anzahl ↔ doppelter Preis) oder nicht?
Info: In einem Schaubild liegen die Größen einer proportionalen Zuordnung auf einer Geraden. Beispiel: Die Verbindung der x-y-Koordinaten (4,2) und (8,4). Siehe folgende Aufgabe.
Aufgabe 6: Ziehe den Punkt A auf die unten aufgeführten x-y-Koordinaten. Ziehe anschließend den Punkt B auf die angegebene x-Koordinate und trage die gesuchte y-Koordinate ein. Die Koordinaten von Punkt A und B bilden eine proportionale Zuordnung.
| a) | b) | c) | d) | e) |
| A(4|2) | A(4|4) | A(5|2) | A(8|2) | A(10|4) |
| B(12|) | B(8|) | B(15|) | B(16|) | B(15|) |
| (x|y) | (x|y) | (x|y) | (x|y) | (x|y) |
Versuche: 0
Aufgabe 7: Ein Meter eines Rohres wiegt kg. Ziehe den orangen Gleiter so, dass das Schaubild zu der Zuordnung Rohrlänge → Gewicht passt. Trage die zugeordneten Werte in die Tabelle ein.
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| kg |
richtig: 0falsch: 0
Aufgabe 8: Mit jeder Gewichtszunahme von 10 g wird eine Federwaage um 2 mm weiter aus ihrem Gehäuse herausgezogen. Trage in die Tabelle ein, wie viele Zentimeter des inneren Stabes der Waage bei den angegebenen Gewichten zu sehen sind. Übertrage die Daten anschließend in das Diagramm.
|

|
||||||||||||||
|
richtig: 0 | falsch: 0 |
| 4 Schokoriegel | ≙ | 2 € | |||
| 1 Schokoriegel | ≙ |
|
|||
| 6 Schokoriegel | ≙ |
|
Die Wertepaare einer proportionalen Zuordnung sind quotientengleich: Dividiert man den Wert der zweiten Größe durch den Wert der ersten Größe, so erhält man bei jedem beliebigen Wertepaar der Zuordnung immer den gleichen Konstanten Wert.
Aufgabe 9: Trage die richtigen Werte ein.
| a) |
Kekse (Packungen) |
Preis
(€) |
b) |
Schokoriegel
(Anzahl) |
Preis
(€) |
c) |
Kuchen (Anzahl) |
Preis (€) |
| 1 | 1 | 1 | ||||||
| 2 | 2,00 | 2 | 2 | |||||
| 3 | 3 | 3 | ||||||
| 4 |
|
4 | 2,00 | 4 | ||||
| 5 |
5 | 5 | ||||||
| 6 |
6 | 6 | 12,00 | |||||
Versuche: 0 |
Versuche: 0 |
Versuche: 0 |
||||||
Aufgabe 10: Vervollständige die Tabelle so, dass eine proportionale Zuordnung entsteht.
| 1. Größe | 1 | 2 | 11 | 15 | 17 | |||
| 2. Größe | 1,5 | 6 | 18 | 24 | ||||
Versuche: 0
Aufgabe 11: Trage die Werte unten in die entsprechenden Textfelder so ein, dass eine proportionale Zuordnung entsteht.
| a) | Anzahl | Preis (€) | b) | Gewicht (kg) | Preis (€) | c) | Zeit (min) | Weg (km) |
| 9 | 45 | 4 | 8 | 5 | 4 | |||
| 3 | 20 | 45 | ||||||
| 15 | 5 | 15 | ||||||
| 5 | 15 | 60 | ||||||
|
Versuche: 0 |
||||||||
| d) | Anzahl | Preis (€) | e) | Menge (l) | Preis (€) | f) | Gewicht (g) | Preis (€) |
| 5 | 20 | 8 | 24 | 300 | 6 | |||
| 1 | 1 | 100 | ||||||
| 8 | 5 | 500 | ||||||
|
Versuche: 0 |
||||||||
Aufgabe 12: Vervollständige die Tabelle so, dass eine proportionale Zuordnung entsteht.
| 1. Größe | 1 | 2 | 11 | 15 | 17 | |||
| 2. Größe | 1,5 | 6 | 18 | 24 |
richtig: 0falsch: 0
Aufgabe 13: Früher wurde die Motorleistung in Pferdestärken (PS) angegeben. Heute führt man die Leistung in Kilowatt (kW) auf. Als üblichen Umrechnungsfaktor verwendet man 1,36. Ein kW entspricht 1,36 PS. Trage die fehlenden Werte ein.
 |
| kW | 1 | 40 | 90 | 100 | 110 | ||
| PS | 1,36 | 102 | 170 |
Versuche: 0
Aufgabe 14: Im Vereinigten Königreich werden Geschwindigkeiten in "Miles per hour" (mph) gemessen. Die Funktion y = 1,6x gibt annähernd an, wie viele "Kilometer pro Stunde" (km/h) dem entsprechenden mph-Wert zuzuordnen sind. Welche Tempoanzeige eines deutschen Autos entspricht den Tempovorgaben der abgebildeten Schilder des Vereinigten Königreichs?
| Tempovorgabe Vereinigtes Königreich (mph) |
||
 |
 |
|
| Tempoanzeige Deutschland (km/h) |
||
Versuche: 0
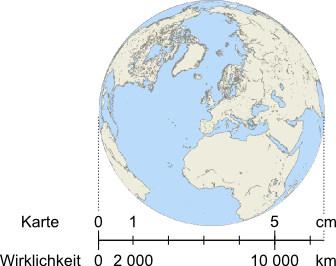
Aufgabe 15: Trage die gesuchten Enfernungen ein.
Erde im Maßstab 1: 200 000 000
1 cm Karte ≙ 2 000 km Wirklichkeit
 |
| Streckenlänge auf der Landkarte |
Länge in der Wirklichkeit | ||
| Maßstab 1 : 200 000 |
Maßstab 1 : 500 000 |
||
| a) | 0 cm | km | km |
| b) | 1 cm | km | km |
| c) | cm | km | 2 km |
| d) | cm | 3 km | km |
richtig: 0falsch: 0
Aufgabe 16: Frank benötigt zum Tanken seines Mopeds eine Mischung aus Öl und Benzin im Verhältnis von 1 : 25. Zu Hause hat er noch eine Öldose mit 500 ml Inhalt stehen. Wie viel Benzin muss er besorgen, damit das Mischungsverhältnis stimmt?
Das Öl aus der Dose muss Frank mit Liter Benzin mischen.
Versuche: 0
Aufgabe 17:
- Trage die richtigen Zahlen unten in die entsprechenden Textfelder ein.
- Wird unten der linke Wert dividiert, dann wird der rechte Wert mit der gleichen Zahl dividiert.
- Wird unten der linke Wert multipliziert, dann wird rechte Wert mit der gleichen Zahl multipliziert.
- Finde die Lösung bei weggeklickter Rechentabelle.
| Aufgabe: | ||||||||||||||||||||||||||||
| Rechnung: |
|
|||||||||||||||||||||||||||
| Antwort: | |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
Aufgabe 18: Ein Laden zeichnet 10 kg Kartoffeln für aus. Wie viel kostet Eli dieser Sorte?
Elli muss für Kartoffeln € bezahlen.
richtig: 0falsch: 0
Aufgabe 19: Herr Mitschke hat mit seinem Auto für eine Fahrt von 600 km 39 Liter Benzin verbraucht. Wie viel Liter Benzin verbraucht sein Wagen pro 100 km.
Der Wagen von Herrn Mitschke benötigt Liter Benzin auf 100 km.
richtig: 0falsch: 0
Aufgabe 20: Ein Wanderer hat einen 9 km langen Weg in 2 ½ Stunden zurückgelegt. In gleichem Tempo läuft er noch 1 ½ Stunden weiter. Welche Strecke hat er insgesamt bewältigt?
Er ist km gelaufen.
Versuche: 0

Aufgabe 21: Eine Lehrerin zahlt den 15 Schülern ihres Fachkurses ein Eis. Dafür werden ihr 27 € berechnet. Als die 26 Schüler ihrer eigenen Klasse das erfahren, wollen sie auch ein Eis. Wie viel bezahlt die Lehrerin dafür?
Bei gleichen Eisportionen zahlt sie für ihre eigene Klasse €.
richtig: 0falsch: 0
Aufgabe 22: Schneewittchen und die sieben Zwerge ist der erste abendfüllende Zeichentrickfilm der Walt-Disney-Studios aus dem Jahr 1937. Für jede Sekunde Film wurden durchschnittlich 18 Bilder benötigt. Rund wie viele Bilder mussten die Disney-Studios für den 83 Minuten langen Film zeichnen? Runde auf Tausender.
Die Disney-Studios zeichneten rund Bilder für diesen Film.
Versuche: 0
Aufgabe 23: Für das Bestreichen von 7 Türen benötigt der Maler 2,8 Liter Farbe. Wie viele Türen kann er mit 2 Litern bestreichen?
Mit 2 Litern Farbe kann der Maler bestreichen.
Versuche: 0
Aufgabe 24: Ein Großhändler von Lebensmitteln kauft einer Obstsorte für . Vor dem Weiterverkauf sortiert er Obst wegen Qualitätsmängeln aus.
| a) | Für welchen Eurobetrag sortiert der Händler mangelhaftes Obst aus? | |
| b) | Die unbeanstandete Ware verkauft der Händler für . Welchen Kilopreis erzielte er damit? | |
| a) | Der Händler sortiert mangelhaftes Obst im Wert von € aus. |
| b) | Der Kilopreis der unbeanstandeten Ware lag bei €. |
richtig: 0falsch: 0
Aufgabe 25: Der Graph zeigt, wie viel Farbe beim Anstreichen der aufgeführten Wandfläche verwendet werden muss.
| a) | Wie viel Farbe werden für 32 Quadratmeter Wandfläche benötigt? |
| b) | Welche Wandfläche kann man mit 12 Litern Farbe bestreichen? |
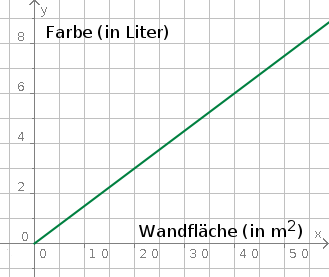
| a) Für 32 m² Wandfläche braucht man Liter Farbe. |
| b) 12 Litern Farbe reichen für m² Wandfläche. |
Versuche: 0
Aufgabe 26: Mit Güterwaggons können Tonnen Kohle transportiert werden. Wie viel Tonnen Kohle können Güterzüge mit je Waggons transportieren?
Die Züge transportieren Tonnen Kohle.
richtig: 0falsch: 0
Aufgabe 27: Pumpen fördern in Stunden Liter Wasser. Wie viel Liter Wasser fördern Pumpen gleicher Leistung in Stunden?
Mit gleichartigen Pumpen werden Liter Wasser in Stunden gefördert.
richtig: 0falsch: 0
Aufgabe 28: Um Teile herzustellen, benötigen Maschinen Stunden. Wie viele dieser Teile können gleichartige Maschinen in Stunden bauen?
In Stunden stellen Maschine Teile her.
richtig: 0falsch: 0
Aufgabe 29: Ein Gastgeber bestellt für sein Fest zwei Party-Pizzen mit den Ausmaßen von je 60 cm x 40 cm. Jede Party-Pizza kostet 19,50 €. Anfänglich überlegte er für seine Gäste Junior-Pizzen zu bestellen. Eine Junior-Pizza hat einen Durchmesser von 26 cm und kostet 6,50 €. Wie viel Geld hätte er für die annähernd gleiche Pizzamenge mehr ausgeben müssen? Rechne sinnvoll mit ganzen Pizzen.
Hätte der Gastgeber die fast gleiche Pizzamenge durch Junior-Pizzen bereitgestellt, hätte er € mehr bezahlt.
Versuche: 0


